لم يتم العثور على نتائج
لا يمكننا العثور على أي شيء بهذا المصطلح في الوقت الحالي، حاول البحث عن شيء آخر.
حاسبة الحجم
تقوم حاسبة الحجم عبر الإنترنت بإجراء عمليات حسابية لـ 11 شكلاً هندسيًا مختلفًا. تدعم الأداة وحدات القياس المختلفة وتوضح خطوات الحل.
الحجم
7238.22945 أمتار3
كان هناك خطأ في الحساب.
فهرس

يحتل كل جسم صلب ثلاثي الأبعاد بعض المساحة. يمكن للمرء أن يفكر في المساحة التي يشغلها هاتفنا الخلوي عند وضعه على الطاولة، أو خزان مياه موضوع على المنزل، أو مجرد كرة قدم في ملعب.
يمكننا تعريف الحجم على أنه المساحة التي يشغلها كائن أو جسم معين. يمكن أن يشير الحجم أيضًا إلى سعة الكائن. بدلاً من التفكير في المساحة التي تشغلها حاوية المياه في مرآبنا، يمكننا التفكير في السعة أو كمية المياه التي يمكن أن تخزنها الحاوية.
يستخدم حساب الحجم في مختلف تخصصات العلوم والرياضيات.
تدعم حاسبة الحجم قياسات متعددة عند حساب الحجم. علاوة على ذلك، تعرض الآلة الحاسبة الصيغة وعملية الحساب خطوة بخطوة. ستوفر هذه المقالة شرحًا بسيطًا ولكنه كافٍ لآلة حاسبة صيغة الحجم والحجم مع أمثلة حقيقية.
الوحدات والقياسات
لتحسين موثوقية ودقة الحساب، نحتاج إلى وحدة قياس قياسية. من أجل التوحيد، نطلب مجموعة معيارية من وحدات القياس، تُعرف بالوحدات القياسية.
حدة حجم النظام الدولي للوحدات (النظام الدولي للوحدات) هي المتر المكعب (متر³). ومع ذلك، يمكن كتابة بعض أحجام الأشياء الصغيرة بوحدات أصغر، مثل السنتيمتر المكعب (سم³) أو المليمتر المكعب (ملليمتر³) إذا كان الجسم صغيرًا جدًا.
من ناحية أخرى، للمستخدم حرية تحديد الوحدة التي تناسب تطبيقه على أفضل وجه. تدعم حاسبة الحجم نظامين للقياس: النظام المتري والوحدات القياسية الإمبراطورية والأمريكية. للمستخدم حرية الاختيار بين الوحدات التالية:
- كيلومتر،
- متر ،
- سم ،
- ملليمتر ،
- ميكرومتر ،
- نانومتر ،
- أنجستروم ،
- اميال،
- ياردة ،
- قدم،
- أو البوصة.
إذا استخدمنا معادلات لحساب الحجم، يجب أن نعمل بوحدة قياس موحدة. لذلك، نقوم بتحويل جميع القياسات إلى نفس الوحدة لتسهيل العمليات الحسابية.
على سبيل المثال، ضع في اعتبارك حساب حجم أسطوانة يبلغ ارتفاعها 75 سم ونصف قطرها 0.5 متر. إما أن نحول الارتفاع إلى متر ونحسب الحجم بالأمتار المكعبة أو نحول نصف القطر إلى سنتيمترات ونوجد الحجم بالسنتيمتر المكعب.
ماذا عن السماح لك بتحديد الارتفاع بالبوصة ونصف القطر بالنانومتر؟ ستقوم الآلة الحاسبة بإجراء تحويل الوحدة هذا وإظهار الخطوات.
ومع ذلك، يمكن للمستخدم اختيار وحدة مختلفة لكل إدخال قياس، وستقوم حاسبة صيغة الحجم بإرجاع الحجم. بالنظر إلى المثال السابق حيث يبلغ ارتفاع الأسطوانة 5 بوصات ونصف القطر 10506070 نانومتر.
سننتقل إلى قسم حاسبة حجم الأسطوانة وإدخال قيم نصف القطر والارتفاع بالوحدات الصحيحة من القائمة المنسدلة.
تقوم الحاسبة أولاً بإرجاع الحجم 2.6874044006564 بوصة³ (بالبوصة المكعبة) و 4.4038667907438E + 22 نانومتر³ (نانومتر مكعب). لماذا هذا؟ نظرًا لأن هذه هي وحدات القياس التي استخدمناها في الإدخال، تفترض الآلة الحاسبة أننا نحتاج إلى حساب الحجم بإحدى هذه الوحدات. يوضح حجم الأسطوانة طريقتين لإجراء الحساب جنبًا إلى جنب مع تحويل الوحدة!
حاسبة الحجم: الأشكال المختلفة والميزات وأمثلة
يمكن أن تختلف طرق حساب الأحجام من رقم إلى آخر. تستخدم بعض الأشكال الهندسية معادلات حسابية قياسية لحساب حجمها بناءً على خصائصها، مثل طول الحافة أو نصف القطر.
الأشكال الهندسية الأخرى أكثر تعقيدًا، ولا يمكنك حساب حجمها مباشرة. في هذه الحالة، يتم استخدام طرق حسابية متقدمة مثل التكامل الهندسي وطرق العناصر المحدودة. تدعم حاسبة الحجم مجموعة كبيرة من الكائنات لحساب حجمها.
الجسم كروي
الكرة هي المكافئ ثلاثي الأبعاد للدائرة؛ مثال على الكرة هو أي كرة مستديرة (بيسبول، كرة سلة، إلخ). تُعطى صيغة الحجم للكرة على النحو التالي:
$$V_{الجسم الكروى}=\frac{4}{3}π r^3$$
يمكننا أن نلاحظ أن حجم الكرة يعتمد فقط على نصف قطر الكرة (r) يتم تعريف نصف القطر على أنه المسافة بين مركز الكرة وأي نقطة على السطح. بالنظر إلى أن نصف قطر كرة البيسبول r=3.65 سم، يمكننا استخدام حجم آلة حاسبة للكرة لإيجاد الحجم:

$$الحجم = \frac{4}{3}πr^3 = \frac{4}{3} × π × 3.65^3 = 203.68882488692 \ سم^3$$
الجسم المخروطى
المخروط شكل هندسي يتكون من قاعدة دائرية مع نقطة أعلاه، يُشار إليها على أنها القمة، حيث تتصل جميع نقاط محيط القاعدة بالقمة بمقاطع خطية. يمكننا تحديد خصائص المخروط بقياسين: نصف قطر القاعدة الدائرية (r) والارتفاع بين مركز القاعدة والقمة (h).
يمكن التعبير عن حجم المخروط على النحو التالي:
$$V_{المخروط}=\frac{1}{3}{π r}^2h$$
r نصف القطر ، و h ارتفاع المخروط
لنفترض أن لديك حفلة عيد ميلاد وترغب في عمل قبعات حفلات مخروطية الشكل والتي سيتم استخدامها بعد ذلك كمخاريط فشار في وقت لاحق أثناء الليل.

إذا قررت عمل قبعات مخروطية نصف قطرها 7.5 سم وارتفاعها 0.45 متر، فيمكنك استخدام حاسبة حجم المخروط لحساب حجم كل قبعة مخروطية.
$$0.45\ أمتار = 45 \ سم$$
$$الحجم = \frac{1}{3}πr^2h = \frac{1}{3} × π × 7.52^2 × 45 = 2650.7188014664 \ سم^3$$
هذا يعني أنه يمكنك وضع الكثير من الفشار في مخروطك في نهاية الحفلة.
المكعب
من لم تسنح له الفرصة للعب بمكعب روبيك؟

هذا جسم هندسي يتكون من ثمانية رؤوس وستة أضلاع متساوية. يعتمد حجم المكعب فقط على طول ضلع المكعب (أ).
$$V_{المكعب}=a^3$$
قررنا شراء 30 مكعب روبيك لمركزنا التنموي حتى يتمكن الأطفال من تحسين قدراتهم المعرفية. ذهبنا إلى المتجر ووجدنا المكعبات المناسبة للتصميم والسعر. طول ضلع المكعب 5.7 سنتيمترات. لسوء الحظ، فإن البائع في المتجر لديه صندوق واحد فقط لتكديس جميع المكعبات لسهولة النقل. الصندوق مكعب طول ضلعه 20 سم. هل ستلائم كل مكعباتنا هذا الصندوق؟
حجم المكعبات:
$$الحجم = 5.7³ = 185.19\ سم³$$
الحجم الإجمالي 30 مكعبًا سيكون
$$185.19 × 30 = 5,555.7\ سم³$$
حجم الصندوق:
$$الحجم = 20³ = 8,000\ سم³$$
قارنا حجم 30 مكعبًا بحجم الصندوق.
$$5,555.7 < 8,000$$
واتضح أن المكعبات تناسب الصندوق تمامًا.
الجسم الأسطواني
الأسطوانة عبارة عن منشور هندسي ذو قاعدة دائرية موحدة كما لو أن دوائر متعددة موضوعة فوق بعضها البعض لتشكيل هذا الشكل الهندسي. مثل المخروط، يتم تحديد خصائص الأسطوانة بنصف قطر الدائرة (r) والارتفاع من السطح السفلي إلى السطح العلوي للأسطوانة (h) يمكن للمرء أن يعبر عن حجم الأسطوانة على النحو التالي:
$$V_{الجسم الأسطواني}=π r^2h$$

دعونا نحسب حجم شمعة أسطوانية مزخرفة حتى يتمكن الحرفي من فهم كمية البارافين التي يحتاجها لصنعها. إذن، سيكون ارتفاع الشمعة 15 سم وقطرها 8 سم. من القطر، يمكننا حساب نصف القطر، الذي سيكون 4 سنتيمترات. لذلك ننتهي بـ:
$$الحجم = πr^2h = π × 4^2 × 15 = 240π = 753.98223686155\ سم^3$$
خزان مستطيل الشكل
هل تتذكر أن المكعب له 12 ضلعًا متساوية الأطوال؟ الخزان المستطيل عبارة عن تباين مكعب حيث تكون جميع الحواف متعامدة ولكن ليست بالضرورة متساوية. يتم تحديد هذا الكائن الهندسي من خلال الطول (l) والعرض (w)، اللذين يمثلان مستطيلًا ثنائي الأبعاد، جنبًا إلى جنب مع الارتفاع (h) الذي ينشئ هذا الامتداد ثلاثي الأبعاد للمستطيل. وبالتالي، يمكن كتابة حجم الخزان المستطيل على النحو التالي:
$$V_{خزان مستطيل}=l × w × h$$
من الأمثلة العالمية على الخزان المستطيل حاوية الشحن. قياسات ISO لحاوية الشحن القياسية هي:
- العرض = 2.43 م
- الارتفاع = 2.59 م
- الطول = 6.06 م أو 12.2 م

نظرًا لأن القياسات قياسية وفقًا لـ ISO، فإن الأحجام تكون قياسية أيضًا. انطلق وقم بتوصيل القياسات بحجم آلة حاسبة خزان المستطيل للعثور على الحجم. قم بإجراء الحسابات لكلا قيم الطول6.06 m و 12.2 m.
$$الحجم = 6.06 × 2.43 × 2.59 = 38.139822\ أمتار³$$
و
$$الحجم = 12.2 × 2.43 × 2.59 = 76.78314\ أمتار³$$
أشكال هندسية ثلاثية الأبعاد أكثر تعقيدًا
يمكننا الجمع بين الأشكال الهندسية الأخرى والأشكال الهندسية الأساسية. ما هو حجم الشكل الذي في هذه الصورة؟
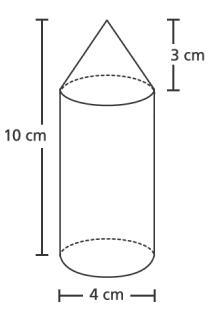
يمكننا أن نرى أن الجسم مكون من أسطوانة ومخروط في الأعلى. لذلك، يمكننا القول أن حجم الجسم هو مجموع حجم الأسطوانة وحجم المخروط:
$$V_{عنصر}=V_{الجسم الأسطواني}+V_{المخروط}$$
يبلغ قطر كل من الأسطوانة والمخروط 4 سم. لذلك يمكننا القول أن
$$r_{الجسم الأسطواني}=r_{المخروط}=\frac{4}{2}=2\ سم$$
إضافة لذلك،
$$h_{عنصر}=h_{الجسم الأسطواني}+h_{المخروط}$$
إذا كان
$$h_{عنصر}=10\ سم$$
و
$$h_{المخروط}=3\ سم$$
يمكننا تفسير أن
$$h_{الجسم الأسطواني}=7\ سم$$
يمكننا الآن إدخال القيم في حاسبة الحجم على النحو التالي:
$$V_{عنصر}=V_{الجسم الأسطواني}+V_{المخروط}=87.96\ سم^3+12.56\ سم^3$$
$$V_{عنصر}=100.52\ سم^3$$
سيساعد هذا المثال على فهم الأشكال الهندسية القادمة التي تدعمها حاسبة الحجم بشكل أفضل.
الكبسولة
الكبسولة هي واحدة من أكثر أشكال الحبوب الطبية شيوعًا. يمكن للمستخدم استخدام المثال السابق لفهم أن الكبسولة تتكون من أسطوانة ذات نصفي كرة على سطحين متقابلين.

يمكن أن يُجمع نصفي الكرة الأرضية في كرة واحدة، ويمكننا القول إن حجم الكبسولة هو مجموع حجم الأسطوانة وحجم الكرة.
$$V_{الكبسولة} = πr^2h + \frac{4}{3}πr^3 = πr^2(\frac{4}{3}r + h)$$
حيث r هو نصف القطر و h هو ارتفاع الجزء الأسطواني.
بفضل حاسبة حجم الكبسولة، لا يتعين عليك حساب حجم الأسطوانة وإضافته إلى حجم الكرة لحساب حجم الكبسولة. يمكن للمستخدم إدخال الارتفاع ونصف القطر مباشرة، وستقوم الآلة الحاسبة بإخراج حجم الكبسولة.
يحاول علماء الصيدلة الذين يقومون بتحليل الأدوية وتطويرها وتصنيعها دائمًا العثور على كميات جيدة من الكبسولات. يجب أن تخزن الكبسولة كمية الدواء المطلوبة لكل كبسولة، لذلك يغير العلماء أبعاد الكبسولة (الارتفاع ونصف القطر) لضبط الحجم وفقًا لذلك.
الغطاء الكروي
أشار المثال السابق إلى نصف الكرة الأرضية على أنها نصف كرة. في هذه الأثناء، الغطاء الكروي هو جزء من الكرة عندما يتم قطع الكرة بواسطة طائرة. نصف الكرة هي حالة خاصة لغطاء كروي حيث تنقسم الكرة إلى جزأين متساويين. وبالتالي، فإن حجم نصف الكرة هو نصف حجم الكرة.
يوضح الشكل أدناه مثالًا لغطاء كروي حيث (r) هو نصف قطر القاعدة ، و (R) هو نصف قطر الكرة و (h) هو ارتفاع الغطاء الكروي. هناك علاقة بين هذه المتغيرات. وبالتالي، يكفي معرفة اثنين من هذه القيم لحساب الثالثة.
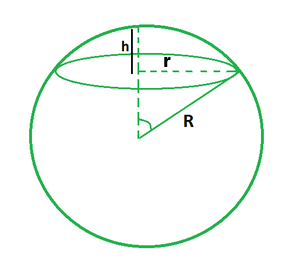
- معطى r و R ؛ $h = R ± \sqrt {R^2 + r^2}$
- معطى r و h ؛ $R = \frac {h^2 + r^2} {2h}$
- معطى R و h ؛ $r = \sqrt {2Rh\ -h^2}$
يمكن كتابة حجم الغطاء الكروي على النحو التالي:
$$V_{غطاء كروي}=\frac{1}{3}π h^2(3R-h)$$
يكفي إدخال اثنين من المتغيرات الثلاثة للغطاء الكروي. على سبيل المثال ، ضع في اعتبارك أن R = 1m و r = 0.25m ، وتجد الآلة الحاسبة أن هناك حجمين محتملين ؛ 0.00313 m³ و 4.1856 m³ . لماذا هذا؟
بتذكر ما يلي
$$h=R±\sqrt{R^2+r^2}$$
يمكننا أن نرى أنه عند إعطاء قيم r و r، يمكن أن يحتوي $h$ على قيمتين
$$h_1=R+\sqrt{R^2+r^2}$$
و
$$h_2=R-\sqrt{R^2+r^2}$$
يوضح هذا وجود قيمة حجم مختلفة عند استخدام $h_1$ و $h_2$.
بالإضافة إلى ذلك، يجب أن تظل المتباينة $R\geq r$ ثابتة دائمًا، أو ستعرض الآلة الحاسبة رسالة خطأ تقول، "لا يمكن أن يكون نصف قطر القاعدة أكبر من نصف قطر الكرة." يكون هذا الخطأ مفيدًا إذا قام المستخدم بخلط القيم R و r.
فروستم مخروطي الشكل
يمكننا الحصول على هذا الشكل عن طريق تقطيع مخروط بقطع أفقي موازٍ لسطحه الدائري. ينتج عن هذا سطحين دائريين واثنين من الأسطح المتوازية.
يمكن تعريف الحجم المخروطي على النحو التالي:
$$V_{فروستم مخروطي}=\frac{1}{3}π h(r^2+rR+R^2)$$
حيث h هو الارتفاع بين مركز السطح السفلي والسطح العلوي ، و r هو نصف قطر السطح العلوي ، و R هو نصف قطر السطح السفلي مثل $R\geq r$.
تخيل أنك ذهبت إلى محل حلويات ورأيت كعكة من الحمم البركانية تقول إنها تحتوي على 35% من الشوكولاتة المذابة.

إذا كنت متحمسًا للرياضيات وتريد ترجمة ذلك إلى مشكلة رياضية، فقد تكون مهتمًا بحجم الشوكولاتة داخل كعكتك. حسنًا، قم بقياس نصف القطر العلوي والسفلي جنبًا إلى جنب مع الارتفاع لحساب حجم الكعكة بأكملها.
افترض أن قياساتك هي r = 16 سم، R = 20سم و h = 10سم.
ثم يمكننا العثور على حجم الكعكة ببساطة عن طريق توصيل القيم في حاسبة حجم الفراغ المخروطي.
$$الحجم=\frac{1}{3}π h(r^2+rR+R^2)=\frac{1}{3}π 10(16^2+16×20+20^2)= 10220.648099679 \ سم^3$$
إلى جانب ذلك، 35% من 10220.65 سم³ هي حوالي 3577.23 سم³ من الشوكولاتة.
الجسم البيضاوي
عندما يتم تشويه الكرة عن طريق القياس الاتجاهي، فإنها تنتج سطحًا يعرف باسم الشكل البيضاوي أو الإهليجي. يمكن للمرء أن يفكر في الشكل البيضاوي باعتباره كرة ممتدة حيث لا تتساوى المسافات بين مركز الشكل البيضاوي والنقاط المختلفة على السطح.
وبالتالي، فإن الشكل البيضاوي له ثلاثة محاور، ويتم تحديد حجم الشكل البيضاوي بالنسبة إلى نصف القطر من المركز إلى كل من هذه المحاور. يتم الإشارة إلى قيم نصف القطر الثلاثة بواسطة a، b و c.
نفكر دائمًا في الكرات المستديرة عندما نتحدث عن الكرات، ولكن الكرات البيضاوية موجودة أيضًا! انظر إلى كرة الرجبي. افترض أن الأبعاد هي a = 9.3سم، b = 9.3سم و c = 14.3سم.
بما أن حجم الشكل البيضاوي معطى على النحو التالي:
$$V_{الجسم البيضاوي}=\frac{4}{3}π abc$$
ترتيب a، b و c غير مهم؛ خلطهم على ما يرام.

باستخدام حاسبة حجم الجسم البيضاوي، يمكننا الحصول على حجم كرة الرجبي الخاصة بنا.
$$الحجم=\frac{4}{3}π abc=\frac{4}{3}× π × 9.3 × 9.3 × 14.3 = 5180.7250468112 \ سم^3$$
الهرم الرباعي
قد يجعلك ذكر الأهرامات تفكر في أهرامات مصر القديمة. يتكون الهرم المربع من قاعدة مربعة ذات قمة حيث تتصل النقاط الموجودة على محيط المربع الأساسي بتلك القمة. يمكن حساب الحجم على النحو التالي:
$$V_{الهرم الرباعي}=\frac{1}{3}a^2h$$
حيث يكون a حافة القاعدة المربعة و h هو الارتفاع من مركز القاعدة المربعة إلى القمة.

نأخذ أبعاد هرم خوفو كما بني في الأصل؛ h = 146.6 m و a = 230.33 m. يمكن حساب حجم هرم خوفو على النحو التالي:
$$الحجم=\frac{1}{3}a^2h = \frac{1}{3}230.33^2 × 146.6 = 2,592,469.9482467\ أمتار^3$$
الأنبوب
على عكس الأسطوانة، يكون للأنبوب قطر خارجي وداخلي. وبالتالي، يجب أن يفسر حجم الأنبوب الفرق في الأقطار.
$$V_{الانبوب}=π\frac{d_1^2-d_2^2}{4}l$$
كما خمنت بالفعل،d₁ و d₂ هما القطران الخارجي والداخلي للأنبوب ، على التوالي l طول الأنبوب.

دعنا نستخدم المعادلة لحساب حجم الحلقة الخرسانية للبئر الذي سنقوم بحفره في منزلنا الريفي. يبلغ ارتفاع الحلقة 0.89 متر، والقطر الخارجي 1.16 مترًا ، والقطر الداخلي 1 متر.
لذلك لدينا الحساب التالي:
$$الحجم=π\frac{1.16^2-1^2}{4} × 0.89 = 0.076896 π = 0.24\ أمتار^3$$