Aucun résultat trouvé
Nous ne pouvons rien trouver avec ce terme pour le moment, essayez de chercher autre chose.
Calculateur de volume
Le calculateur de volume en ligne est capable de calculer le volume de 11 figures géométriques différentes. L'outil est compatible avec différentes unités de mesure et fournit les étapes de la solution.
Volume
7238.22945 mètres3
Il y avait une erreur avec votre calcul.
Table des Matières

Tous les objets tridimensionnels solides occupent un certain espace. On peut penser à l'espace occupé par notre téléphone portable lorsqu'il est posé sur la table, à un réservoir d'eau dans le voisinage ou simplement à un ballon de football sur un terrain.
On peut définir le volume comme l'espace occupé par un objet. Le volume peut également faire référence à la capacité de l'objet. Au lieu de penser à l'espace que le réservoir d'eau occupe dans notre garage, nous pouvons penser à sa capacité, c’est-à-dire la quantité d'eau que le réservoir peut stocker.
Le calcul du volume est utilisé dans diverses disciplines des sciences et des mathématiques.
Le calculateur de volume est compatible avec plusieurs mesures lors du calcul du volume. De plus, le calculateur fournit la formule ainsi que le processus de calcul étape par étape. Cet article fourni une explication simple mais suffisante du volume et du calculateur de formule de volume avec des exemples pratiques.
Unités et mesures
Afin d’améliorer la fiabilité et la précision de nos mesures, nous avons besoin d'une unité de mesure standard. Afin d’assurer l'uniformité, nous avons besoin d'un ensemble normalisé d'unités de mesure, appelé unités standard.
L'unité de volume SI (Système International d'unités) est le mètre cube m³. Cependant, les volumes de certains petits objets peuvent être écrits en unités plus petites, telles que les centimètres cubes cm³ ou les millimètres cubes mm³ si l'objet est très petit.
Cependant, l'utilisateur est libre de spécifier l'unité qui correspond le mieux à son application. Le calculateur de volume prend en charge deux systèmes de mesure : le système métrique ainsi que les unités impériales et américaines. L'utilisateur a la liberté de choisir entre les unités suivantes :
- kilomètres,
- mètres,
- centimètres,
- millimètres,
- micromètres,
- nanomètres,
- angströms,
- miles,
- yards (verges),
- pieds,
- pouces.
Lors de l’utilisation de formules pour calculer un volume, il est important de travailler avec des unités de mesure homogènes. Par conséquent, il est généralement nécessaire de convertir toutes les mesures dans la même unité pour faciliter les calculs.
Par exemple : considérons le calcul du volume d'un cylindre d'une hauteur de 75 cm et d'un rayon de 0,5 m. Il nous faut soit convertir la hauteur en mètres et calculer le volume en mètres cubes, soit convertir le rayon en centimètres et calculer le volume en centimètres cubes.
Ne serait-il pas pratique de pouvoir définir la hauteur en pouces et le rayon en nanomètres ? Le calculateur effectuera lui-même cette conversion d'unité et en affichera les étapes.
Grâce à ce calculateur, l'utilisateur peut choisir une unité différente pour chaque entrée de mesure, et le calculateur de formule de volume se chargera de renvoyer le volume.
Prenons l'exemple d’un cylindre dont la hauteur est de 5 pouces et le rayon est de 10 506 070 nanomètres. Il suffit de naviguer vers la section du calculateur de volume de cylindre, de saisir les valeurs du rayon et de la hauteur, et de sélectionner les unités correspondantes dans la liste déroulante.
Le calculateur renvoie le volume, d’abord en pouces cubes : 2,6874044006564 pouces³, et ensuite en nanomètres cubes : 4,4038667907438E+22 nanomètres³. Pourquoi donc ? Parce que ce sont les unités de mesure que nous avons utilisées dans notre entrée, le calculateur suppose donc que nous avons besoin que le volume soit calculé avec l'une de ces unités. Le calculateur montre les deux manières d'effectuer le calcul ainsi que la conversion d'unité !
Le calculateur de volume : portée, fonctionnalités et exemples
Les méthodes de calcul des volumes peuvent varier d’une figure géométrique à l'autre. Certaines figures géométriques utilisent des formules arithmétiques standard pour calculer leur volume en fonction de leurs propriétés, telles que la longueur des arêtes ou le rayon.
D'autres figures géométriques sont plus complexes et on ne peut pas calculer leur volume directement. Dans ce cas, des méthodes de calcul avancées telles que l'intégration géométrique ou la méthode des éléments finis sont utilisées. Le calculateur de volume prend en charge une large gamme d'objets pour calculer leur volume.
Sphère
Une sphère est l'équivalent tridimensionnel d'un cercle ; un exemple de sphère est n'importe quel ballon rond (baseball, ballon de basket, etc.). La formule du volume d'une sphère est comme suit :
$$V_{Sphère}=\frac{4}{3}π r^3$$
On peut observer que le volume d'une sphère ne dépend que du rayon de la sphère (r). Le rayon est défini comme la distance entre le centre de la sphère et tout point de la surface. Sachant qu'une balle de baseball a un rayon r = 3,65 cm, nous pouvons utiliser le calculateur de sphère pour trouver le volume :

$$Volume = \frac{4}{3}πr^3 = \frac{4}{3} × π × 3,65^3 = 203,68882488692 \ centimètres^3$$
Cône
Un cône est une figure géométrique composée d'une base circulaire et d'un sommet, qu’on appelle aussi l’apex, où tous les points situés sur la circonférence de la base sont reliés au sommet par des segments de ligne. On peut définir les propriétés du cône avec deux mesures : le rayon de la base circulaire (r) et la hauteur entre le centre de la base et le sommet (h).
Le volume d'un cône peut être exprimé par :
$$V_{Cône}=\frac{1}{3}{π r}^2h$$
r est le rayon et h est la hauteur du cône
Imaginons que vous avez une fête d'anniversaire et que vous voulez faire des chapeaux de fête en forme de cône qui seront ensuite utilisés comme cornets pour le pop-corn plus tard dans la soirée.

Si vous décidez de faire des chapeaux coniques avec un rayon de 7,5 cm et une hauteur de 0,45 m, vous pouvez utiliser le calculateur de volume de cône pour calculer le volume de chaque chapeau conique.
0,45 mètre = 45 centimètres
$$Volume = \frac{1}{3}πr^2h = \frac{1}{3} × π × 7,52^2 × 45 = 2650,7188014664 \ centimètres^3$$
Cela signifie que vous pouvez mettre cette quantité de pop-corn dans votre cornet à la fin de la fête.
Cube
Qui n'a pas eu la chance de jouer avec un Rubik's Cube ?

C'est un objet géométrique avec 8 sommets et 6 côtés égaux. Le volume d'un cube dépend uniquement de la longueur du côté du cube (a).
$$V_{cube}=a^3$$
Nous avons décidé d'acheter 30 Rubik's cubes pour notre centre de développement afin que les enfants puissent améliorer leurs capacités cognitives. Nous sommes allés au magasin et avons trouvé des cubes de bonne qualité et à un bon prix. La longueur du côté du cube est de 5,7 centimètres. Malheureusement, le vendeur du magasin n'a qu'une seule boîte pour empiler tous les cubes afin de les transporter plus facilement. La boîte est cubique et faot 20 centimètres de côté. Est-ce que tous nos cubes rentreront dans cette boîte ?
Le volume des cubes :
$$Volume = 5,7³ = 185,19\ centimètres³$$
Le volume total de 30 cubes serait :
$$185,19 × 30 = 5.555,7\ centimètres³$$
Le volume de la boîte :
$$Volume = 20³ = 8.000\ centimètres³$$
Nous avons donc comparé le volume des 30 cubes au volume de la boîte :
$$5.555,7 < 8.000$$
Et il s’avère que les cubes rentreraient parfaitement dans la boîte.
Cylindre
Un cylindre est un prisme géométrique avec une base circulaire uniforme, c’est comme si plusieurs cercles étaient entassés les uns sur les autres pour former cette figure géométrique. Comme le cône, les propriétés du cylindre sont définies par le rayon du cercle à sa base (r) et la hauteur entre la surface inférieure et la surface supérieure du cylindre (h). On peut exprimer le volume d'un cylindre comme suit :
$$V_{Cylindre}=π r^2h$$

Calculons maintenant le volume d'une bougie cylindrique décorative afin que l'artisan puisse déterminer la quantité de paraffine dont il aura besoin pour la fabriquer. La hauteur de la bougie sera de 15 centimètres et le diamètre de 8 centimètres. À partir du diamètre, nous pouvons calculer le rayon, qui est de 4 centimètres. Donc on se retrouve avec :
$$Volume = πr^2h = π × 4^2 × 15 = 240π = 753,98223686155\ centimètres^3$$
Réservoir rectangulaire
Un réservoir rectangulaire est une variante d’un cube où tous les bords sont perpendiculaires mais pas nécessairement égaux. Cet objet géométrique est défini par une longueur (l) et une largeur (w ), qui représentent un rectangle bidimensionnel, ainsi qu'une hauteur (h) qui crée l’extension tridimensionnelle du rectangle. Ainsi, le volume du réservoir rectangulaire peut s'écrire comme suit :
$$V_{Réservoir\ rectangulaire}=l × w × h$$
Un exemple universel de réservoir rectangulaire est le conteneur maritime. Les mesures ISO standard des conteneurs maritimes sont :
- Largeur = 2,43 m
- Hauteur = 2,59 m
- Longueur = 6,06 m ou 12,2 m

Étant donné que les mesures sont standard selon ISO, le volume sera également standard. Allez-y et saisissez les mesures dans le volume du calculateur de réservoir rectangulaire pour trouver le volume. Effectuez les calculs pour les deux valeurs de longueur, 6,06 m et 12,2 m.
$$Volume = 6,06 × 2,43 × 2,59 = 38,139822\ mètres³$$
Et :
$$Volume = 12,2 × 2,43 × 2,59 = 76,78314\ mètres³$$
Figures géométriques tridimensionnelles plus complexes
Nous pouvons générer d'autres figures géométriques en combinant des figures géométriques de base. Quel est le volume de cette figure ?
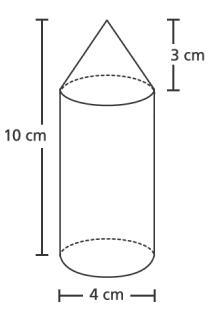
Nous pouvons voir que l'objet est composé d'un cylindre et d'un cône sur le dessus. On peut donc dire que le volume de l'objet est la somme du volume du cylindre et du volume du cône :
$$V_{objet}=V_{cylindre}+V_{cône}$$
Le cylindre et le cône ont tous deux un diamètre de 4 cm. Ainsi, nous pouvons dire que
$$r_{cylindre}=r_{cône}=\frac{4}{2}=2\ cm$$
En outre :
$$h_{objet}=h_{cylindre}+h_{cône}$$
Étant donné que :
$$h_{objet}=10\ cm$$
Et :
$$h_{cône}=3\ cm$$
On peut en déduire que :
$$h_{cylindre}=7\ cm$$
Nous pouvons maintenant saisir les valeurs dans le calculateur de volume comme suit :
$$V_{objet}=V_{cylindre}+V_{cône}=87,96\ cm^3+12,56\ cm^3$$
$$V_{objet}=100,52\ cm^3$$
Cet exemple vous permettra de mieux comprendre les figures géométriques ci-dessous qui sont prises en charge par le calculateur de volume.
Gélule
La gélule est l'une des formes les plus courantes de médicament. L'utilisateur peut se servir de l'exemple précédent pour comprendre qu'une gélule est constituée d'un cylindre avec deux hémisphères sur deux surfaces opposées.

Les deux hémisphères peuvent s'additionner pour former une seule sphère, et on peut dire que le volume d'une gélule est la somme du volume d'un cylindre et du volume d'une sphère.
$$V_{Gélule} = πr^2h + \frac{4}{3}πr^3 = πr^2(\frac{4}{3}r + h)$$
Où r est le rayon et h est la hauteur de la partie cylindrique.
Grâce au calculateur de volume de gélule, vous n'avez plus besoin de calculer le volume du cylindre et de l'additionner à celui de la sphère pour calculer le volume de la gélule. L'utilisateur peut saisir directement la hauteur et le rayon, et le calculateur affichera le volume de la gélule.
Les scientifiques spécialisés en pharmacologie qui analysent, développent et fabriquent des médicaments ont besoin de calculer les volumes des gélules. La gélule doit stocker la quantité de médicament requise par gélule, de sorte que les scientifiques varient les dimensions de la gélule (hauteur et rayon) pour ajuster le volume en conséquence.
Calotte sphérique
L'exemple précédent faisait référence à l'hémisphère prise comme une demi-sphère. Pour sa part, une calotte sphérique est une portion de la sphère coupée par un plan. L'hémisphère est un cas particulier de calotte sphérique pour lequel la sphère est divisée en deux parties égales. Ainsi, le volume d'un hémisphère est la moitié du volume d'une sphère.
La figure ci-dessous montre un exemple de calotte sphérique où (r) est le rayon de la base, (R) est le rayon de la sphère et (h) est la hauteur de la calotte sphérique. Or, il existe une relation entre ces variables. Il suffit donc de connaître seulement deux de ces valeurs pour calculer la troisième.
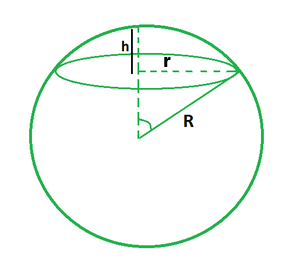
- Soit r et R ; $h=R±\sqrt{R^2+r^2}$
- Soit r et h ; $R=\frac{h^2+r^2}{2h}$
- Soit R et h ; $r=\sqrt{2Rh\ -h^2}$
Sachant que :
- r est le rayon de la base,
- R est le rayon de la sphère,
- h est la hauteur de la calotte sphérique.
Le volume d'une calotte sphérique peut s'écrire comme suit :
$$V_{Calotte\ sphérique}=\frac{1}{3}π h^2(3R-h)$$
Il suffit de saisir deux des trois variables de la calotte sphérique dans le calculateur. Par exemple, considérons que R = 1m et r = 0,25m, le calculateur trouve deux volumes possibles ; 0,00313 m³ et 4,1856 m³. Pourquoi donc ?
Rappelons-nous que :
$$h=R±\sqrt{R^2+r^2}$$
On peut voir que lorsqu'on donne les valeurs de r et r, h peut avoir deux valeurs
$$h_1=R+\sqrt{R^2+r^2}$$
Ou :
$$h_2=R-\sqrt{R^2+r^2}$$
Cela explique le fait que le calculateur retourne deux volumes différents : un pour $h_1$ et un pour $h_2$.
De plus, l'inégalité R ≥ r doit toujours être vrai, sinon le calculateur renverra un message d'erreur indiquant que "le rayon de la base ne peut pas être supérieur au rayon de la sphère". Cette erreur est utile si l'utilisateur mélange par accident les valeurs R et r.
Tronc conique
On peut obtenir cette figure en découpant un cône de manière horizontale et parallèle à sa surface circulaire. Il en résulte deux surfaces circulaires et deux surfaces parallèles.
Le volume d’un tronc conique peut être défini comme :
$$V_{Tronc\ conique}=\frac{1}{3}π h(r^2+rR+R^2)$$
Où h est la hauteur entre le centre des surfaces inférieure et supérieure, r est le rayon de la surface supérieure et R est le rayon de la surface inférieure tel que R ≥ r.
Imaginez que vous alliez dans une pâtisserie et que vous voyiez un gâteau coulant au chocolat avec l’indication qu'il contient 35 % de chocolat fondu.

Si vous êtes un vrai passionné de mathématiques et que vous souhaitez faire de cela un problème mathématique, il pourrait être intéressant de calculer le volume de chocolat à l'intérieur de votre gâteau. Pour ce faire, mesurez le rayon supérieur et inférieur ainsi que la hauteur pour calculer le volume de l'ensemble du gâteau.
Supposons que les mesures soient r = 16 cm, R = 20 cm et h = 10 cm.
Ensuite, nous pouvons déterminer le volume du gâteau en saisissant les valeurs dans le calculateur de volume de tronc conique.
$$Volume=\frac{1}{3}π h(r^2+rR+R^2)=\frac{1}{3}π 10(16^2+16×20+20^2)= 10220.648099679 \ centimètres^3$$
Or, 35% de 10 220,65 cm³ représente environ 3 577,23 cm ³ de chocolat.
Ellipsoïde
Lorsqu'une sphère est déformée par agrandissement ou réduction directionnelle, elle produit une surface appelée ellipsoïde. On peut considérer un ellipsoïde comme une sphère étirée pour laquelle les distances entre le centre de l'ellipsoïde et différents points de la surface ne sont pas égales.
Ainsi, l'ellipsoïde a trois axes, et le volume de l'ellipsoïde est déterminé en fonction des rayons qui vont du centre de l'ellipsoïde jusqu’à chacun de ces trois axes. Ces trois rayons sont désignés par a, b et c.
On pense toujours à des sphères rondes quand on parle de ballons, mais les ballons ellipsoïdaux existent aussi ! Prenez par exemple le ballon de rugby. Supposons que les dimensions sont a = 9,3 cm, b = 9,3 cm et c = 14,3 cm.
Le volume d'un ellipsoïde est donné par :
$$V_{Ellipsoïde}=\frac{4}{3}π abc$$
L'ordre de a, b et c n'a pas d'importance ; on peut les interchanger.

En utilisant le calculateur de volume d’un ellipsoïde, nous pouvons obtenir le volume de notre ballon de rugby.
$$Volume=\frac{4}{3}π abc=\frac{4}{3}× π × 9,3 × 9,3 × 14,3 = 5180,7250468112 \ centimètres^3$$
Pyramide carrée
La mention de pyramides pourrait vous faire penser aux anciennes pyramides d'Égypte. Une pyramide carrée se compose d'une base carrée avec un sommet, pour laquelle les points situés sur la circonférence du carré de base sont reliés à ce sommet. Le volume peut être calculé comme suit :
$$V_{Pyramide\ carrée}=\frac{1}{3}a^2h$$
Avec a le bord de la base carrée et h la hauteur entre le centre de la base carrée et le sommet.

Prenons les dimensions de la pyramide de Khéops telle qu'elle fut construite à l'origine ; h = 146,6 m et a = 230,33 m. Le volume de la pyramide de Khéops peut être calculé comme suit :
$$Volume=\frac{1}{3}a^2h = \frac{1}{3}230,33^2 × 146,6 = 2.592.469,9482467\ mètres^3$$
Tube
Contrairement à un cylindre, un tube a un diamètre extérieur et un diamètre intérieur. Ainsi, le volume du tube doit tenir compte de la différence entre ces diamètres.
$$V_{tube}=π\frac{d_1^2-d_2^2}{4}l$$
Comme vous l'avez déjà deviné, d₁ et d₂ sont respectivement les diamètres extérieur et intérieur du tube. l est la longueur du tube.

Utilisons cette formule pour calculer le volume d’un anneau de béton utilisé pour le puits que nous allons creuser sur la propriété de notre chalet. La hauteur de notre anneau est de 0,89 mètre, le diamètre extérieur est de 1,16 mètre et le diamètre intérieur est de 1 mètre.
Nous avons donc le calcul suivant :
$$Volume=π\frac{1,16^2-1^2}{4} × 0,89 = 0,076896 π = 0,24\ meters^3$$