ไม่พบผลลัพธ์
เราไม่พบอะไรกับคำที่คุณค้นหาในตอนนี้, ลองค้นหาอย่างอื่นดู
เครื่องคำนวนปริมาตร
เครื่องคำนวนปริมาตรออนไลน์ทำการคำนวนรูปทรงเลขาคณิตที่แตกต่างกัน 11 แบบ เครื่องมือนี้รองรับหน่วยการวัดที่แตกต่างกันและสาธิตขั้นตอนการแก้ปัญหา
ปริมาณ
7238.22945 เมตร3
เกิดข้อผิดพลาดกับการคำนวณของคุณ
สารบัญ

วัตถุสามมิติทึบทุกอันจะใช้พื้นที่บางส่วน ใครๆก็สามารถนึกถึงพื้นที่ที่โทรศัพท์มือถือของเราใช้เมื่อวางบนโต๊ะ ถังเก็บน้ำที่วางอยู่ใกล้ๆ หรือเพียงแค่เล่นฟุตบอลในสนาม
เราสามารถกำหนดปริมาตรเป็นพื้นที่ที่วัตถุครอบครองได้ ปริมาตรยังหมายถึงความจุของวัตถุอีกด้วย แทนที่จะคิดถึงพื้นที่ที่ภาชนะบรรจุน้ำอยู่ในโรงรถของเรา เราสามารถคิดถึงความจุหรือปริมาณน้ำที่ภาชนะบรรจุน้ำสามารถกักเก็บได้
การคำนวนปริมาตรใช้ในสาขาวิชาวิทยาศาสตร์และคณิตศาสตร์ที่หลากหลาย
เครื่องคำนวณปริมาตรรองรับการวัดหลายรายการเมื่อคำนวณปริมาตร นอกจากนี้เครื่องคำนวนยังแสดงสูตรและขั้นตอนการคำนวณแบบทีละขั้นตอนอีกด้วย บทความนี้จะให้คำอธิบายที่เรียบง่ายแต่เพียงพอเกี่ยวกับเครื่องคำนวณปริมาตรและสูตรปริมาตรพร้อมตัวอย่างจริง
หน่วยและการวัด
เพื่อปรับปรุงความน่าเชื่อถือและความแม่นยำของการตัดสินของเรา เราจำเป็นต้องมีหน่วยการวัดมาตรฐาน เพื่อความสม่ำเสมอ เราต้องการชุดหน่วยการวัดที่เป็นมาตรฐานหรือที่เรียกว่าหน่วยมาตรฐาน
หน่วยปริมาตร SI (ระบบหน่วยสากล) คือลูกบาศก์เมตร ม.³ อย่างไรก็ตาม ปริมาตรของวัตถุขนาดเล็กบางชนิดสามารถเขียนเป็นหน่วยที่เล็กกว่าได้ เช่น ลูกบาศก์เซนติเมตร ซม.³ หรือลูกบาศก์มิลลิเมตร มม.³ หากวัตถุนั้นเล็กเกินไป
ในทางกลับกัน ผู้ใช้มีอิสระที่จะระบุหน่วยที่เหมาะกับการใช้งานของตนมากที่สุด เครื่องคำนวนปริมาตรรองรับระบบการวัดสองระบบ: ระบบเมตริก หน่วยอิมพีเรียล และหน่วยวัดของสหรัฐอเมริกา ผู้ใช้มีอิสระในการเลือกระหว่างหน่วยต่อไปนี้:
- กิโลเมตร
- เมตร
- เซนติเมตร
- มิลลิเมตร
- ไมโครเมตร
- นาโนเมตร
- อังสตรอม
- ไมล์
- หลา
- ฟุต
- นิ้ว
ถ้าเราใช้สูตรในการคำนวณปริมาตร เราจะต้องทำงานกับหน่วยวัดที่เป็นแบบเดียวกัน ดังนั้นเราจึงมักจะแปลงหน่วยวัดทั้งหมดให้เป็นหน่วยเดียวกันเพื่อให้การคำนวนง่ายขึ้น
ยกตัวอย่างเช่น ลองคำนวณปริมาตรของทรงกระบอกที่มีความสูง 75 ซม. และมีรัศมี 0.5 ม. เราแปลงความสูงเป็นเมตรแล้วคำนวณปริมาตรเป็นลูกบาศก์เมตร หรือแปลงรัศมีเป็นเซนติเมตรแล้วหาปริมาตรเป็นลูกบาศก์เซนติเมตร
ลองให้คุณกำหนดความสูงเป็นนิ้วและรัศมีเป็นนาโนเมตรดูไหม? เครื่องคิดเลขจะทำการแปลงหน่วยนี้และแสดงขั้นตอนต่างๆ
ด้วยเครื่องคำนวนนี้ ผู้ใช้สามารถเลือกหน่วยที่แตกต่างกันสำหรับอินพุตการวัดแต่ละรายการ และเครื่องคำนวณสูตรปริมาตรจะคำนวนปริมาตร
ลองพิจารณาตัวอย่างที่ความสูงของทรงกระบอกคือ 5 นิ้วและมีรัศมี 10506070 นาโนเมตร เราจะไปที่ส่วนเครื่องคำนวณปริมาตรกระบอกสูบและป้อนค่ารัศมีและความสูงด้วยหน่วยที่ถูกต้องจากรายการแบบเลื่อนลง
เครื่องคิดเลขจะส่งกลับปริมาตรเป็น 2.6874044006564 นิ้ว³ (เป็นลูกบาศก์นิ้ว) และ 4.4038667907438E+22 นาโนเมตร³ (ลูกบาศก์นาโนเมตร) ก่อน ทำไมเป็นอย่างนั้น? เนื่องจากสิ่งเหล่านี้เป็นหน่วยการวัดที่เราใช้ในการป้อนข้อมูล เครื่องคิดเลขจึงถือว่าเราจำเป็นต้องคำนวณปริมาตรด้วยหน่วยใดหน่วยหนึ่งเหล่านี้ ปริมาตรกระบอกสูบแสดงสองวิธีในการคำนวณพร้อมกับการแปลงหน่วย!
เครื่องคำนวoปริมาตร: ขอบเขต คุณสมบัติ และตัวอย่าง
วิธีการคำนวณปริมาตรอาจแตกต่างกันไปในแต่ละรูป รูปทรงเรขาคณิตบางรูปทรงใช้สูตรเลขคณิตมาตรฐานในการคำนวณปริมาตรตามคุณสมบัติ เช่น ความยาวขอบหรือรัศมี
รูปทรงเรขาคณิตอื่นๆนั้นซับซ้อนกว่า และคุณไม่สามารถคำนวoปริมาตรได้โดยตรง ในกรณีนี้ จะใช้วิธีการคำนวoขั้นสูง เช่น วิธีอินทิเกรตเชิงเรขาคณิต และวิธีการไฟไนต์เอลิเมนต์ เครื่องคำนวoปริมาตรรองรับวัตถุที่หลากหลายเพื่อคำนวoปริมาตร
ทรงกลม
ทรงกลมนั้นเทียบเท่ากับสามมิติของวงกลม ตัวอย่างของทรงกลมคือลูกบอลกลมใดๆ (เบสบอล บาสเก็ตบอล ฯลฯ) สูตรปริมาตรของทรงกลมได้รับดังนี้:
$$V_{ทรงกลม}=\frac{4}{3}π r^3$$
เราจะสังเกตได้ว่าปริมาตรของทรงกลมขึ้นอยู่กับรัศมีของทรงกลม (r) เท่านั้น รัศมีถูกกำหนดให้เป็นระยะทางระหว่างจุดศูนย์กลางของทรงกลมกับจุดใดๆบนพื้นผิว เนื่องจากลูกเบสบอลมีรัศมี r = 3.65 ซม. เราจึงสามารถใช้ปริมาตรของเครื่องคำนวณทรงกลมเพื่อหาปริมาตรได้:

$$ปริมาณ = \frac{4}{3}πr^3 = \frac{4}{3} × π × 3.56^3 = 188.9899034802 \ เซนติเมตร^3$$
กรวย
กรวยเป็นรูปทรงเรขาคณิตที่ประกอบด้วยฐานทรงกลมและจุดยอด ซึ่งแสดงเป็นยอด โดยที่จุดเส้นรอบวงฐานทั้งหมดเชื่อมต่อกับยอดด้วยส่วนของเส้นตรง เราสามารถกำหนดคุณสมบัติของกรวยได้ด้วยการวัดสองแบบ ได้แก่ รัศมีของฐานวงกลม (r) และความสูงระหว่างจุดศูนย์กลางของจุดศูนย์กลางฐานกับยอด (h)
ปริมาตรของกรวยสามารถแสดงได้ดังนี้:
$$V_{กรวย}=\frac{1}{3}{π r}^2h$$
r คือรัศมี และ h คือความสูงของกรวย
สมมติว่าคุณมีงานเลี้ยงวันเกิดและต้องการทำหมวกปาร์ตี้รูปทรงกรวยทำเอง ซึ่งจะใช้เป็นโคนป๊อปคอร์นในตอนกลางคืน

หากคุณตัดสินใจที่จะทำหมวกทรงกรวยที่มีรัศมี 7.5 ซม. และสูง 0.45 ม. คุณสามารถใช้เครื่องคำนวนปริมาตรทรงกรวยเพื่อคำนวณปริมาตรของหมวกทรงกรวยแต่ละอันได้
0.45 เมตร = 45 เซนติเมตร
$$ปริมาณ = \frac{1}{3}πr^2h = \frac{1}{3} × π × 7.52^2 × 45 = 2650.7188014664 \ เซนติเมตร^3$$
ซึ่งหมายความว่าคุณสามารถใส่ป๊อปคอร์นจำนวนเท่านี้ลงในกรวยของคุณเมื่อสิ้นสุดปาร์ตี้ได้
ลูกบาศก์
ใครไม่มีโอกาสได้เล่นลูกบาศก์รูบิคบ้าง?

นี่คือวัตถุเรขาคณิตที่มีจุดยอด 8 จุดและมีด้านเท่ากัน 6 ด้าน แม้ว่าสี่เหลี่ยมจัตุรัสจะมีขอบสี่ด้านที่เท่ากัน แต่ลูกบาศก์ก็มีขอบที่เท่ากันถึง 12 ขอบ ดังนั้น ปริมาตรของลูกบาศก์จึงขึ้นอยู่กับความยาวของด้านของลูกบาศก์ (a) เท่านั้น
$$V_{ลูกบาศก์}=a^3$$
เราตัดสินใจซื้อลูกบาศก์รูบิค 30 ลูกให้กับศูนย์พัฒนาการของเรา เพื่อให้เด็กๆได้พัฒนาความสามารถทางปัญญาของตนเอง เราไปที่ร้านและพบลูกบาศก์ที่เหมาะกับดีไซน์และราคา ความยาวของด้านของลูกบาศก์คือ 5.7 เซนติเมตร น่าเสียดายที่พนักงานขายที่ร้านมีเพียงกล่องๆเดียวสำหรับการบรรจุลูกบาศก์ทั้งหมดเพื่อการขนส่งที่ง่ายดาย กล่องเป็นทรงลูกบาศก์ ยาวด้านละ 20 เซนติเมตร ลูกบาศก์ทั้งหมดของเราจะพอดีกับกล่องนั้นหรือไม่?
ปริมาตรของลูกบาศก์:
$$ปริมาณ = 5.7³ = 185.19\ เซนติเมตร³$$
ปริมาตรรวมของลูกบาศก์ 30 ลูกจะเท่ากับ
$$185.19 × 40 = 5,555.7\ เซนติเมตร³$$
ปริมาตรของกล่อง:
$$ปริมาณ = 20³ = 8,000\ เซนติเมตร³$$
เราเปรียบเทียบปริมาตรของลูกบาศก์ 30 ลูกกับปริมาตรของกล่อง
$$5,555.7 < 8,000$$
และปรากฎว่าลูกบาศก์จะพอดีกับกล่องพอดี
ทรงกระบอก
ทรงกระบอกคือปริซึมทางเรขาคณิตที่มีฐานเป็นวงกลมสม่ำเสมอ เหมือนกับว่ามีวงกลมหลายวงวางซ้อนกันเพื่อสร้างเป็นรูปทรงเรขาคณิต เช่นเดียวกับกรวย คุณสมบัติของทรงกระบอกถูกกำหนดโดยรัศมีของวงกลม (r) และความสูงจากพื้นผิวด้านล่างถึงพื้นผิวด้านบนของทรงกระบอก (h) เราสามารถแสดงปริมาตรของทรงกระบอกได้ดังนี้:
$$V_{ทรงกระบอก}=π r^2h$$

ลองคำนวณปริมาตรของเทียนทรงกระบอกตกแต่งเพื่อให้ช่างฝีมือเข้าใจว่าจะต้องทำพาราฟินมากแค่ไหน ดังนั้นเทียนของเราจะมีความสูง 15 เซนติเมตรและมีเส้นผ่านศูนย์กลาง 8 เซนติเมตร จากเส้นผ่านศูนย์กลางเราสามารถคำนวณรัศมีได้ซึ่งจะเท่ากับ 4 เซนติเมตร ดังนั้นเราจึงลงเอยด้วย:
$$ปริมาณ = πr^2h = π × 4^2 × 15 = 240π = 753.98223686155\ เซนติเมตร^3$$
ถังสี่เหลี่ยม
ถังสี่เหลี่ยมเป็นรูปแบบลูกบาศก์ที่ขอบทั้งหมดตั้งฉากกันแต่ไม่จำเป็นต้องเท่ากัน วัตถุทางเรขาคณิตนี้กำหนดโดยความยาว (l) และความกว้าง (w) ซึ่งเป็นตัวแทนของสี่เหลี่ยมผืนผ้าสองมิติ พร้อมด้วยความสูง (h) ที่สร้างส่วนขยายสามมิติของสี่เหลี่ยมผืนผ้า ดังนั้น ปริมาตรของถังทรงสี่เหลี่ยมจึงสามารถเขียนได้ดังนี้:
$$V_{ถังสี่เหลี่ยม}=l × w × h$$
ตัวอย่างที่เป็นสากลของถังทรงสี่เหลี่ยมคือตู้คอนเทนเนอร์ การวัดแบบ ISO ของตู้คอนเทนเนอร์ขนส่งสินค้ามาตรฐานคือ:
- ความกว้าง = 2.43 ม.
- ความสูง = 2.59 ม.
- ความยาว = 6.06 ม. หรือ 12.2 ม.

เนื่องจากการวัดเป็นมาตรฐานตามมาตรฐาน ISO ปริมาตรจึงเป็นมาตรฐานเช่นกัน ดำเนินการต่อและใส่หน่วยวัดลงในปริมาตรของเครื่องคำนวนถังสี่เหลี่ยมเพื่อค้นหาปริมาตร ทำการคำนวนทั้งค่าความยาว 6.06 ม. และ 12.2 ม.
$$ปริมาณ = 6.06 × 2.43 × 2.59 = 38.139822\ เมตร³$$
และ
$$ปริมาณ = 12.2 × 2.43 × 2.59 = 76.78314\ เมตร³$$
รูปทรงเรขาคณิตสามมิติที่ซับซ้อนมากขึ้น
เราสามารถรวมรูปทรงเรขาคณิตอื่นๆเข้ากับรูปทรงเรขาคณิตพื้นฐานได้ รูปทรงนี้มีปริมาตรเท่าใด?
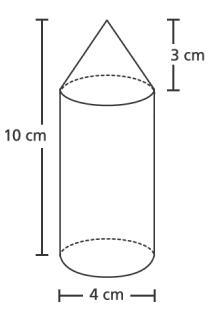
เราจะเห็นได้ว่าวัตถุนั้นประกอบด้วยทรงกระบอกและมีกรวยอยู่ด้านบน ดังนั้นเราจึงสามารถพูดได้ว่าปริมาตรของวัตถุคือผลรวมของปริมาตรของทรงกระบอกและปริมาตรของกรวย:
$$V_{วัตถุ}=V_{กระบอก}+V_{กรวย}$$
ทั้งทรงกระบอกและกรวยมีเส้นผ่านศูนย์กลาง 4 ซม. ดังนั้นเราจึงสามารถพูดได้ว่า
$$r_{กระบอก}=r_{กรวย}=\frac{4}{2}=2\ เซนติเมตร$$
นอกจากนี้
$$h_{วัตถุ}=h_{กระบอก}+h_{กรวย}$$
ระบุว่า
$$h_{วัตถุ}=10\ เซนติเมตร$$
และ
$$h_{กรวย}=3\ เซนติเมตร$$
เราตีความได้ว่า
$$h_{กระบอก}=7\ เซนติเมตร$$
ตอนนี้เราสามารถใส่ค่าลงในเครื่องคำนวนปริมาตรได้ดังนี้:
$$V_{วัตถุ}=V_{กระบอก}+V_{กรวย}=87.96\ เซนติเมตร^3+12.56\ เซนติเมตร^3$$
$$V_{วัตถุ}=100.52\ เซนติเมตร^3$$
ตัวอย่างนี้จะช่วยให้เข้าใจรูปทรงเรขาคณิตที่กำลังจะมาถึงซึ่งเครื่องคำนวนปริมาตรรองรับได้ดีขึ้น
แคปซูล
แคปซูลเป็นหนึ่งในยาเม็ดทางการแพทย์ที่พบได้บ่อยที่สุด ผู้ใช้สามารถใช้ตัวอย่างก่อนหน้านี้เพื่อทำความเข้าใจว่าแคปซูลประกอบด้วยทรงกระบอกที่มีซีกโลกสองอันบนพื้นผิวสองอันที่อยู่ตรงข้ามกัน

ซีกโลกทั้งสองสามารถรวมกันได้เป็นทรงกลมเดียว และเราสามารถพูดได้ว่าปริมาตรของแคปซูลคือผลรวมของปริมาตรของทรงกระบอกและปริมาตรของทรงกลม
$$V_{แคปซูล} = πr^2h + \frac{4}{3}πr^3 = πr^2(\frac{4}{3}r + h)$$
โดยที่ r คือรัศมีและ h คือความสูงของส่วนทรงกระบอก
ด้วยเครื่องคำนวนปริมาตรแคปซูล คุณไม่จำเป็นต้องคำนวนปริมาตรของทรงกระบอกและบวกเข้ากับทรงกลมเพื่อคำนวนปริมาตรของแคปซูล ผู้ใช้สามารถป้อนความสูงและรัศมีได้โดยตรง จากนั้นเครื่องคิดเลขจะส่งออกปริมาตรของแคปซูล
นักวิทยาศาสตร์ด้านเภสัชกรรมที่วิเคราะห์ พัฒนา และผลิตยามักจะพยายามค้นหาแคปซูลในปริมาณที่เหมาะสมอยู่เสมอ แคปซูลควรเก็บปริมาณยาที่ต้องการต่อแคปซูล ดังนั้นนักวิทยาศาสตร์จึงเปลี่ยนขนาดของแคปซูล (ความสูงและรัศมี) เพื่อปรับปริมาตรให้เหมาะสม
หมวกทรงกลม
ตัวอย่างที่แล้วเรียกซีกโลกว่าครึ่งทรงกลม ในขณะเดียวกัน ฝาครอบทรงกลมเป็นส่วนหนึ่งของทรงกลมเมื่อทรงกลมถูกตัดด้วยระนาบ ซีกโลกเป็นกรณีพิเศษของฝาครอบทรงกลมที่ทรงกลมถูกแบ่งออกเป็นสองส่วนเท่าๆกัน ดังนั้น ปริมาตรของซีกโลกจึงเท่ากับครึ่งหนึ่งของปริมาตรของทรงกลม
รูปด้านล่างแสดงตัวอย่างหมวกทรงกลม โดยที่ (r) คือรัศมีของฐาน (R) คือรัศมีของทรงกลม และ (h) คือความสูงของฝาครอบทรงกลม มีความสัมพันธ์ระหว่างตัวแปรเหล่านี้ ดังนั้นจึงเพียงพอที่จะทราบค่าสองค่าเหล่านี้เพื่อคำนวณค่าที่สาม
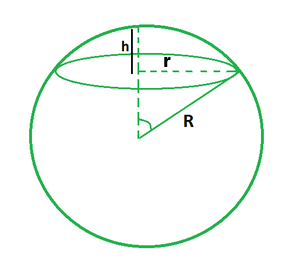
- ให้ r และ R; $h=R±\sqrt{R^2+r^2}$
- ให้ r และ h; $R=\frac{h^2+r^2}{2h}$
- ให้ R และ h; $r=\sqrt{2Rh\ -h^2}$
ที่ซึ่ง:
- r คือรัศมีของฐาน
- R คือรัศมีของทรงกลม
- h คือความสูงของหมวกทรงกลม
ปริมาตรของหมวกทรงกลมสามารถเขียนได้ดังนี้:
$$V_{หมวกทรงกลม}=\frac{1}{3}π h^2(3R-h)$$
เพียงป้อนสองในสามตัวแปรของหมวกทรงกลมก็เพียงพอแล้ว ตัวอย่างเช่น พิจารณาว่า R = 1 ม. และ r = 0.25 ม. เครื่องคำนวนจะค้นหาปริมาตรที่เป็นไปได้สองปริมาตร 0.00313 ม.³ และ 4.1856 ม.³ ทำไมเป็นอย่างนั้น?
ระลึกถึงสิ่งต่อไปนี้
$$h=R±\sqrt{R^2+r^2}$$
เราจะเห็นได้ว่าเมื่อกำหนดค่า r และ r แล้ว h สามารถมีค่าได้สองค่า
$$h_1=R+\sqrt{R^2+r^2}$$
และ
$$h_2=R-\sqrt{R^2+r^2}$$
สิ่งนี้จะอธิบายว่ามีค่าปริมาตรที่แตกต่างกันเมื่อใช้ $h_1$ และ $h_2$
นอกจากนี้ ค่าอสมการ R ≥ r ควรคงไว้เสมอ มิฉะนั้นเครื่องคำนวนจะแสดงข้อความแสดงข้อผิดพลาดว่า "รัศมีฐานต้องไม่ใหญ่กว่ารัศมีลูกบอล" ข้อผิดพลาดนี้จะมีประโยชน์หากผู้ใช้ผสมค่า R และ r
ฟรัสดัมทรงกรวย
เราสามารถได้รูปทรงนี้โดยการตัดกรวยโดยให้มีการตัดแนวนอนขนานกับพื้นผิวทรงกลม ส่งผลให้มีพื้นผิวทรงกลมสองอันและพื้นผิวขนานกันสองอัน
ปริมาตรฟรัสดัมทรงกรวยสามารถกำหนดได้เป็น:
$$V_{ฟรัสดัมทรงกรวย}=\frac{1}{3}π h(r^2+rR+R^2)$$
โดยที่ h คือความสูงระหว่างจุดศูนย์กลางของพื้นผิวด้านล่างและด้านบน r คือรัศมีพื้นผิวด้านบน และ R คือรัศมีพื้นผิวด้านล่าง โดยที่ R ≥ r
ลองนึกภาพคุณไปที่ร้านขายขนมและเห็นเค้กลาวาบอกว่ามีช็อกโกแลตละลายอยู่ 35%

หากคุณเป็นคนที่คลั่งไคล้คณิตศาสตร์มากและอยากแปลงสิ่งนี้ให้กลายเป็นโจทย์คณิตศาสตร์ คุณอาจจะสนใจปริมาณช็อกโกแลตในเค้กของคุณ วัดรัศมีด้านบนและด้านล่างพร้อมกับความสูงเพื่อคำนวณปริมาตรของเค้กทั้งหมด
สมมติว่าค่าที่วัดคือ r = 16 ซม. R = 20 ซม. และ h = 10 ซม.
จากนั้นเราสามารถหาปริมาตรเค้กได้โดยการใส่ค่าในเครื่องคำนวนปริมาตรฟรัสตัมทรงกรวย
$$ปริมาณ=\frac{1}{3}π h(r^2+rR+R^2)=\frac{1}{3}π 10(16^2+16×20+20^2)= 10220.648099679 \ เซนติเมตร^3$$
นอกจากนี้ 35% ของ 10,220.65 ซม.³ คือประมาณ 3,577.23 ซม.³ ของช็อคโกแล็ต
ทรงรี
เมื่อทรงกลมเปลี่ยนรูปตามทิศทาง จะทำให้เกิดพื้นผิวที่เรียกว่าทรงรี เราสามารถนึกถึงทรงรีว่าเป็นทรงกลมที่ยืดออก โดยที่ระยะห่างระหว่างจุดศูนย์กลางของทรงรีและจุดต่างๆ บนพื้นผิวไม่เท่ากัน
ดังนั้นทรงรีจึงมีสามแกน และปริมาตรของทรงรีถูกกำหนดโดยสัมพันธ์กับรัศมีจากจุดศูนย์กลางไปยังแต่ละแกนเหล่านี้ ค่ารัศมีทั้งสามจะแสดงด้วย a b และ c
ทุกครั้งที่เราพูดถึงลูกบอล เรามักจะนึกถึงทรงกลมทรงกลม แต่ทรงกลมทรงรีก็มีอยู่เช่นกัน! ดูลูกรักบี้สิ สมมติว่าขนาดคือ a = 9.3 ซม. b = 9.3 ซม. และ c = 14.3 ซม.
ปริมาตรของทรงรีถูกกำหนดเป็น:
$$V_{ทรงรี}=\frac{4}{3}π abc$$
ลำดับของ a b และ c นั้นไม่สำคัญ การผสมมันก็โอเค

เมื่อใช้เครื่องคำนวนปริมาตรทรงรี เราจะได้ปริมาตรของลูกรักบี้
$$ปริมาณ=\frac{4}{3}π abc=\frac{4}{3}× π × 9.3 × 9.3 × 14.3 = 5180.7250468112 \ เซนติเมตร^3$$
ปิรามิดสี่เหลี่ยมจตุรัส
การกล่าวถึงปิรามิดอาจทำให้คุณนึกถึงปิรามิดโบราณของอียิปต์ ปิรามิดสี่เหลี่ยมจัตุรัสประกอบด้วยฐานสี่เหลี่ยมจัตุรัสที่มียอดซึ่งจุดบนเส้นรอบวงของฐานสี่เหลี่ยมจัตุรัสเชื่อมต่อกับยอดนั้น ปริมาณสามารถคำนวณได้ดังนี้:
$$V_{ปิรามิดสี่เหลี่ยมจตุรัส}=\frac{1}{3}a^2h$$
โดยที่ a เป็นขอบของฐานสี่เหลี่ยม และ h คือความสูงจากศูนย์กลางฐานสี่เหลี่ยมถึงยอด

เราใช้มิติของปิรามิดคูฟูตามที่ถูกสร้างขึ้นแต่แรก h = 146.6 ม. และ a = 230.33 ม. ปริมาตรของปิรามิดคูฟูสามารถคำนวณได้ดังนี้:
$$ปริมาณ=\frac{1}{3}a^2h = \frac{1}{3}230.33^2 × 146.6 = 2,592,469.9482467\ เมตร^3$$
ท่อ
ท่อมีเส้นผ่านศูนย์กลางภายนอกและภายในต่างจากทรงกระบอก ดังนั้นปริมาตรของท่อจะต้องคำนึงถึงความแตกต่างของเส้นผ่านศูนย์กลางด้วย
$$V_{ท่อ}=π\frac{d_1^2-d_2^2}{4}l$$
ดังที่คุณเดาได้แล้ว d₁ และ d₂ คือเส้นผ่านศูนย์กลางภายนอกและภายในของท่อ ตามลำดับ l คือความยาวของท่อ

ลองใช้สูตรคำนวณปริมาตรของวงแหวนคอนกรีตของบ่อที่เราจะขุดบนกระท่อมของเรา ความสูงของวงแหวนของเราคือ 0.89 เมตร เส้นผ่านศูนย์กลางภายนอกคือ 1.16 เมตร และเส้นผ่านศูนย์กลางภายในคือ 1 เมตร
ดังนั้นเราจึงได้การคำนวนดังนี้:
$$ปริมาณ=π\frac{1.16^2-1^2}{4} × 0.89 = 0.076896 π = 0.24\ เมตร^3$$