Quadratic Equation Calculator

The Quadratic Equation Calculator

Quadratic equations are a significant part of school and university mathematics curricula. For instance, the quadratic equation solution provides various information such as the rates of change, upturns, and downturns of the function. Finding the solution to a quadratic equation requires performing a set of algebraic and arithmetic operations. Although the solution has a standard form, it takes some time to do the math manually.

The online quadratic formula calculator is an easy-to-use tool that instantly provides the user with the solution to a quadratic equation. This free tool provides the answers and presents the steps applied when solving the equation. Consequently, the user will conceptualize the problem solving, numerical results, and a step-by-step guide through the solution.

Quadratic Equations

A quadratic equation sometimes referred to as a quadratic function or second-degree polynomial, is an algebraic equation with a general form of ax²+bx+c=0 where x is an unknown variable to be found. The terms a and b are the coefficients of x² and x, respectively, while C is a constant. The word "quad" or "second-degree" comes from the fact that the highest exponent of the variable x is 2, as in x². We can show some examples of quadratic equations below.

$$2x²-4x+0.5=0$$

$$-3x²+\frac{1}{3}x+6=0$$

The equation 2x²=0 is also a quadratic equation, with b=0 and c=0. However, 2x+3=0 does not represent a quadratic equation since the quadratic term ax² is not found in the equation. As shown in the previous examples, the values of A, B, and C can be positive/negative integers or decimals (fractions) such that a≠0.

Solving Quadratic Equations

The number of possible solutions to an equation equals the highest exponent value in the equation. A quadratic equation can have a maximum of two solutions in this context. One way to solve a quadratic function is using the quadratic formula stated in equation (1).

$$x₁=\frac{-b+\sqrt{b²-4ac}}{2a}\ \ \ \ \ \ \ ;\ \ \ x₂=\frac{-b-\sqrt{b²-4ac}}{2a}$$ (1)

You can write the compact form for the quadratic formula as:

$$x=\frac{-b±\sqrt{b²-4ac}}{2a}$$

This is a straightforward solution where the user can plug the values A, B, and C to get the value of x₁ and x₂. According to the value of the discriminant denoted by the term under the square root b²-4ac, the number and nature of the solution changes. We can discuss three cases:

• If the discriminant is positive; b²-4ac>0, then two real solutions exist (x₁≠x₂)
• If the discriminant is zero; b²-4ac=0, then one real solution exists (x₁=x₂)
• If the discriminant is negative; b²-4ac<0, then two complex solutions exist (x₁≠x₂)

We will provide an example of each case in the Examples section.

Graphically, on an x-y coordinate plane, where y is a function of x, the reader can visually realize the solution(s) of a quadratic function as the x-coordinate(s) of the points(s) where the function y crosses the x-axis.

Using the Quadratic Formula Calculator

The quadratic solver calculator can solve all quadratic equations, regardless of the nature of the solution (real or complex). The calculator takes three inputs: the values of A, B, and C. In some cases, the user might have to perform some manipulations to the equation before using the calculator.

In 2x² = x + 3, the user has to simply move the terms from the right-hand side to the left-hand side. As a result we get 2x²-x-3=0, where a = 2, b = -1, and c = - 3.

Furthermore, considering 4(x²-0.2x)=1, the user has to expand the parenthesis by writing 4x²-0.8x=1, then move the terms on the left-hand side to the right-hand to put the equation in the general form as 4x²-0.8x-1=0 where a = 4, b=-0.8 and c=-1.

Examples

In this section, three examples can explain the three possible cases of the quadratic equation solution using the quadratic equations calculator.

Example 1: Two Real Solutions

It is required to find the solution(s) of the quadratic function y₁ given as y₁=x²-8x+12 and shown in Figure 1.

Intuitively, the aim is to find the x-coordinate(s) of the points(s) where the function y₁ crosses the x-axis – if any exists.

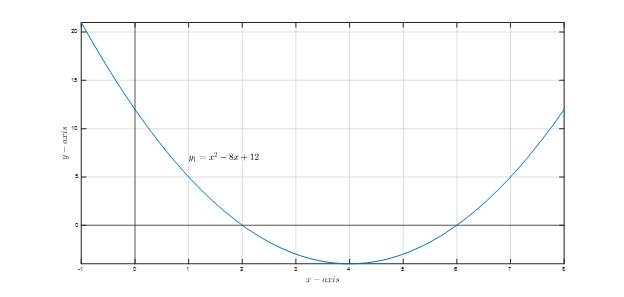
Figure 1: Plot of y₁=x²-8x+12

First, the function is equated to zero ( y₁ is replaced by 0), yielding to x²-8x+12=0. It is seen that the last equation is in the standard quadratic equation form where a=1, b=-8, and c=12. We can directly use the quadratic equation formula calculator.

Checking the value of the discriminant b²-4ac=(-8)²-4(1)(12)=16>0, the quadratic function should have two real solutions. After clicking the calculate button, the calculator provides the numerical solution and the solution steps using the equation's quadratic formula (1).

It is essential to highlight that after entering the values of A, B, and C, the calculator shows the equation. The user might consider verifying that the displayed equation is the same as the equation in hand to avoid entry mistakes.

• Equation: x²-8x+12=0

• Solution: x₁=2 and x₂=6

• Steps:

$$x = \frac {-b ± \sqrt{b² - 4ac}}{2a}=\frac{-(-8) ±\sqrt{(-8)^2-4×1×12}}{2×1}=\frac{8 ±\sqrt{16}}{2}=4 ±2=6 \ or \ 2$$

The solution is thus x₁=2 and x₂=6. We can graphically validate the results by inspecting the function intersection with the x-axis. Figure 2 shows that the function crosses the x-axis in the before-mentioned points.

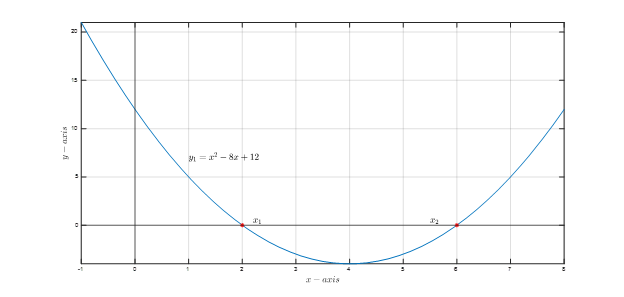
Figure 2: Plot of y₁=x²-8x+12

Example 2: One Real Solution

Considering another function, y₂-3x²+25=-4x²+10x. Before using the calculator, an initial step would be isolating y₂ on one side and collecting all the other terms on the other side as y₂=-4x²+10x+3x²-25. Equating y₂ to zero and doing the arithmetic operations, the general form is obtained as -x²+10x-25=0 with a=-1, b=10, and c=-25.

The discriminant is equal to zero b²-4ac=(10)²-4(-1)(-25)=0, so, the user would expect a single solution. Then, We can use the quadratic formula calculator to find x₁=x₂=5.

• Equation: -x²+10x–25=0

• Solution: x = 5

• Steps:

$$x = \frac{-b ± \sqrt{b² - 4ac}}{2a} = \frac{-10±{\sqrt{10^2 – 4 × (-1) × (-25)}}}{2×-1}=\frac{-10± \sqrt{0}}{-2} = 5$$

Figure 3 shows the plot of y₂ where it is seen that the function crosses the x-axis at one point.

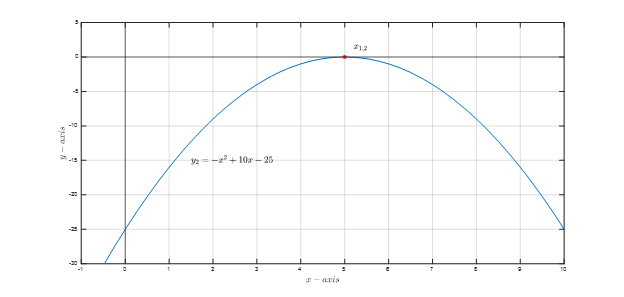
Figure 3: y₂=-x²+10x-25

Example 3: Two Complex Solutions

Finally, y₃=x²-4x+8 is studied to show how a quadratic function can have two complex solutions. Figure 4 shows that y₃ does not cross the x-axis.

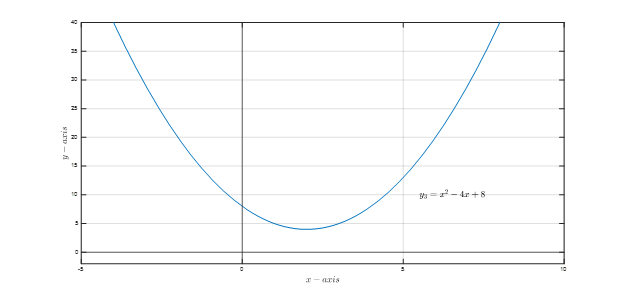
Figure 4: y₃=x²-4x+8

Looking at b²-4ac=(-4)²-4(1)(8)=-16<0 which indicates the existence of two complex solutions, but what are complex numbers?

A complex number is a number that is expressed in the form of a combination of real and imaginary numbers and takes the form of a+ib.

In this case,'i' in complex numbers stands for the imaginary unit, representing the square root of -1.

The term A denotes the real part of the complex number (Re). On the other hand, ib is the imaginary number (Im) where i=√-1.

The square root will contain a negative number when the term b²-4ac is less than zero. Thus, taking the square root of a negative number requires using complex numbers.

Back to finding the solution of x²-4x+8=0; the calculator solves the equation and finds x₁=2+2i and x₂=2-2i.

• Equation: x²–4x+8=0

• There are two possible solutions: x=2±2i

• Steps:

$$x = \frac{-b ± \sqrt{b² – 4ac}}{2a} = \frac{-(-4) ± \sqrt{(-4)^2 – 4 × 1 × 8}}{2 × 1} = \frac{4 ± \sqrt{-16}}{2} = 2 ± 2i$$

Scope of Use and Tips

The quadratic formula calculator is designed for students in schools and universities or anyone looking for a quick solution to a quadratic function. Quadratic functions can be found in engineering, economics, agriculture, etc.

While using the tool is straightforward, the user should be able to perform basic arithmetic operations to put the equation in the standard quadratic form ax²+bx+c=0 to use the tool. Moreover, it is preferable (not a prerequisite) to be familiar with complex numbers since the solution of a quadratic equation might be a pair of complex numbers.

The user might also be interested in using some plotting tools to visualize the function and its solutions.