Cylinder Volume Calculator

This versatile circular cylinder calculator instantly finds the missing characteristics of a cylinder based on your known parameters. Whether you need to determine the cylinder height, radius, volume, lateral surface area, or total surface area, this tool has you covered. Simply input two known parameters to calculate the rest. Thanks to its flexibility, you can seamlessly use this tool as a cylinder volume calculator and a cylinder surface area calculator.

List of parameters

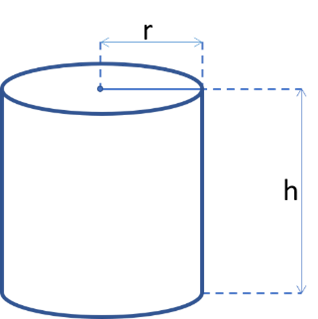
This calculator uses the following notation for circular cylinder characteristics:

• h – the height of the cylinder
• r – base radius
• V – volume
• L – lateral surface area
• A – total surface area

The additional characteristics used in the calculations include:

• T – top surface area
• B – base surface area (B = T)

Directions for use

To use the calculator, simply select your desired calculation type from the drop-down menu at the top. The available options are:

• Calculate V, L, A | Given r, h
• Calculate h, L, A | Given r, V
• Calculate h, V, A | Given r, L
• Calculate r, V, A | Given h, L
• Calculate r, L, A | Given h, V

After selecting your calculation type, enter the corresponding known values into the input fields.

For example, if you need to calculate the total surface area, lateral surface area, and volume of a cylinder, and you already know the cylinder's height and base radius, choose "Calculate V, L, A | Given r, h". Then, enter the cylinder height (h) and base radius (r) into the designated fields.

You can also customize the value of π (Pi) used in the calculations. The default value is 3.1415926535898. Note that the calculator incorporates a safeguard: if you enter a value too far from the true mathematical value of π (for example, if you input π = 10), it will automatically revert to the default value of 3.1415926535898 to ensure accuracy.

Finally, select your preferred units of measurement (meters, centimeters, millimeters, miles, yards, feet, inches) and choose the number of significant figures (up to 9) for rounding your final answers.

Once you have configured your inputs, press "Calculate".

Formulas

Cylinder volume

You can find the volume of a cylinder by multiplying its base area by its height. The base of a circular cylinder is a circle with a radius r. The surface area of this circle is calculated as πr². Therefore, the cylinder volume, V, can be found using the following formula:

V = πr²h

Lateral surface area

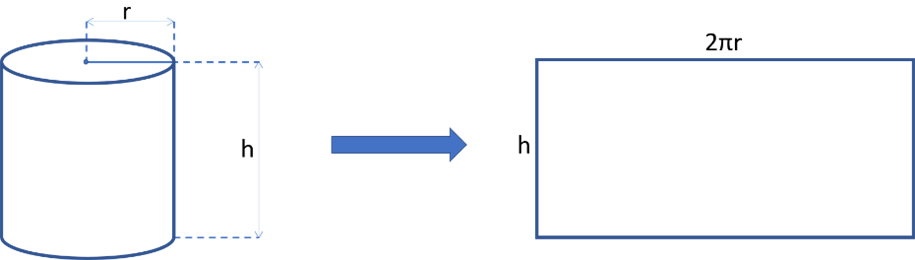
A cylinder's lateral surface area is the area occupied by its curved side. If you were to "unroll" the side surface of a cylinder onto a flat plane, it would form a rectangle. One side of this rectangle is equal to the cylinder's height (h), and the other side is equal to the circumference of the base circle. Since the area of a rectangle is found by multiplying the lengths of its sides, and the circumference of the base circle is 2πr, the lateral surface area of a cylinder can be calculated with this formula:

L = 2πrh

Base surface area (and top surface area)

A circular cylinder's top surface area, T, and base surface area, B, are identical because the top and bottom are equal circles. Thus, B = T, and both can be found using the standard formula for the area of a circle:

B = T = πr²

The total surface area of a cylinder

A cylinder's total surface area encompasses all of its exterior surfaces: the top, the bottom, and the lateral (side) surface. Therefore, the total surface area of a cylinder, A, is the sum of these individual areas:

A = B + T + L = πr² + πr² + 2πrh = 2πr² + 2πrh = 2πr(r + h)

Calculation algorithms

Let's break down the algorithms this cylinder calculator uses for each specific calculation type.

Calculate V, L, A | Given r, h

In this straightforward scenario, the calculator directly applies the standard formulas presented above to find the missing cylinder characteristics.

Calculate h, L, A | Given r, V

The standard formulas require both h and r. In this situation, the radius (r) and volume (V) are known, but we need to find the height (h). By rearranging the volume formula, we can solve for h:

h = V / (πr²)

Once h is calculated, the tool uses both h and r to compute the remaining parameters.

Calculate h, V, A | Given r, L

Here, the radius (r) and lateral surface area (L) are given, and we need to find the height (h) to use the standard cylinder formulas. We can extract h from the lateral area formula:

h = L / 2πr

With both h and r now known, the calculator easily computes the missing values.

Calculate r, V, A | Given h, L

In this case, the height (h) and lateral surface area (L) are known, and we must find the radius (r). Using the lateral area formula, r can be found as follows:

r = L / 2πh

Now that both h and r are established, the remaining parameters are calculated.

Calculate r, L, A | Given h, V

Here, the height (h) and volume (V) are known, and we need to solve for the radius (r). Rearranging the volume formula gives us:

$$r=\sqrt{\frac{V}{πh}}$$

With h and r both known, the tool proceeds to calculate the missing characteristics.

Real-life applications

Calculating the various characteristics of a circular cylinder has numerous practical applications in everyday life and industry. For instance, determining the total surface area is necessary when calculating the exact amount of material needed to manufacture a cylindrical container or tank. Lateral surface area calculations are frequently used in construction, engineering, and plumbing to correctly size pipes and tubes. Furthermore, knowing a cylinder's volume is essential for estimating the capacity of a container, ensuring you know exactly how much liquid or solid material can be safely stored inside.

Example

What is the volume of a cylindrical water tank with a height of 5 meters and a base diameter of 4 meters?

Solution

To use the standard formula for cylinder volume, we must know the height of the cylinder and its base radius. We are given the height (h = 5 m) and the base diameter (d = 4 m). The base radius can be found by dividing the diameter in half:

r = d/2 = 4/2 = 2

Now we have all the necessary parameters: h = 5 and r = 2. Assuming that π = 3.14, the volume is calculated as follows:

V = πr²h = 3.14 × (2)² × 5 = 3.14 × 4 × 5 = 62.8

Answer

The cylindrical water tank has a volume of 62.8 m³.