No results found
We can’t find anything with that term at the moment, try searching something else.
Tank Volume Calculator
The tank volume calculator finds the total volume of various tank shapes in gallons, liters, and cubic meters. It calculates the liquid volume of partially filled tanks.
| 0% Full | Total Capacity | Filled Volume |
|---|---|---|
| U.S. Gallons | 6639.39 | 3319.67 |
| Imp. Gallons | 5528.44 | 2764.2 |
| Liters | 25132.8 | 12566.3 |
| Cubic Meters | 25.1328 | 12.5663 |
| Cubic Feet | 887.556 | 443.775 |
There was an error with your calculation.
Table of Contents

This tank capacity calculator finds the total volume of the given tank and the volume of the liquid in the tank for situations when the tank is not completely full. The tank shapes include:
- Horizontal cylinder
- Vertical cylinder
- Rectangular prism
- Horizontal oval tank
- Vertical oval tank
- Horizontal capsule tank
- Vertical capsule tank
- Horizontal semi-elliptical tank with 2:1 semi-elliptical tank heads
- Horizontal tank with dish heads
The final answers are calculated in U. S. gallons, imperial gallons, liters, cubic meters, and cubic feet.
Directions for use
First, choose the required tank shape from the drop-down menu to use this tank calculator. Then input the known values into the corresponding fields. Each tank shape has its list of values. If the tank is not full, enter the filled depth. Filled depth is the only optional value, all other values must be filled in. After inserting all values, press "Calculate."
The calculator will return the total capacity of a tank and the filled volume.
This liquid volume calculator accepts integers, decimals, fractions, and numbers in e-notation as inputs. All input values representing dimensions have to be greater than zero. The filled depth must be greater than or equal to zero.
Calculating the capacity of a tank
Let's look at the formulas for calculating the total volume of a tank. The symbols for the known dimensions will be demonstrated on the corresponding images for each tank shape.
Horizontal cylinder tank
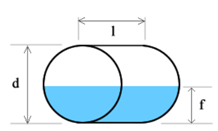
To find the volume of a horizontal cylinder, we have to multiply its base area by its length. If the base is a circle of radius r, its area can be found as πr². Multiplying that by the length, we will get the total tank volume:
V = π × r² × l
Since r = d/2, the above formula can be re-written as follows:
V = π × r² × l = π × (d/2)² × l
Vertical cylinder tank
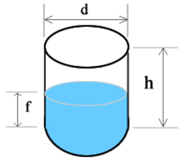
The formula for the total volume of a vertical cylinder is the same as the formula for the horizontal cylinder, where the length, l, is replaced with the height, h:
V = π × r² × h = π × (d/2)² × h
Rectangular tank (rectangular prism)
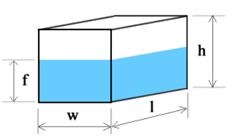
This tank shape is widely known as "rectangular tank,"; however, this is not its official name. The rectangle is a 2D shape, and the tank is a rectangular prism. To find the volume of a rectangular prism, we have to multiply all three dimensions of the tank – width, length, and height:
V = w × l × h
Horizontal oval tank
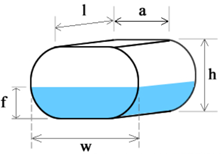
This calculator defines an oval tank as a cylindrical tank with bases in a stadium shape. A stadium shape is defined as a rectangle with semicircles at opposite sides. To find the tank volume, we must multiply the base area by length.
Let's find the base area. The base area is represented by a stadium shape, as shown in the image below. The surface area of the stadium shape can be found by adding the rectangle surface area and the two semi-circles surface areas. Two semi-circles form one circle with radius r. Therefore, their combined area will be πr². The inner rectangle has sides with the following lengths: a and 2r. Its surface area can be found as 2ar.
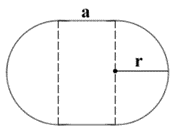
The total surface area of the stadium shape can be found as πr² + 2ar.
The volume of a horizontal oval tank with the stadium shape base and length l can be found as follows:
V = (πr² + 2ar) × l
Since the calculator works in terms of the height of the cylinder, h, and h = 2r, the above formula can be re-written as follows:
r = h/2
V = (π(h/2)² + 2a(h/2)) × l = ((πh²)/4 + ah) × l
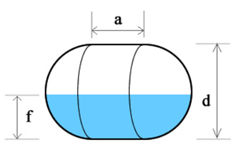
Vertical oval tank
While the volume of filled liquid for this tank will be different from the corresponding filled volume of the horizontal oval tank, the total volume formula is the same:
V = (πr² + 2ar) × l
In this case, w = 2r, and r = w/2, therefore, the formula can be re-written as follows:
V = (π(w/2)² + 2a(w/2)) × l = ((πw²)/4 + aw) × l
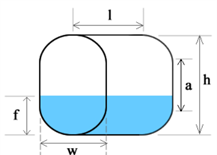
Horizontal Capsule Tank
The horizontal capsule tank is defined as a combination of a cylindrical section and two hemispherical end caps. To calculate its volume, we need to sum the volumes of the cylinder and the two hemispheres.
- Cylinder Volume: The central part of the capsule is a cylinder. If the cylinder has a radius r and side length (cylindrical section length) L, its volume is given by
$$V_{cylinder} = \pi r^2 L$$
- Hemispherical End Caps Volume: Each hemisphere has a radius r. The volume of a single hemisphere is
$$\frac{2}{3}\pi r^3$$
Since there are two hemispheres, their combined volume is
$$2 \times \frac{2}{3}\pi r^3 = \frac{4}{3}\pi r^3$$
Therefore, the total volume V of the horizontal capsule tank is the sum of the volume of the cylinder and the two hemispheres:
$$V = V_{cylinder} + V_{hemispheres} = \pi r^2 L + \frac{4}{3}\pi r^3$$
Given that the radius r is half the diameter d i.e.,
$$r = \frac{d}{2}$$
the formula can be rewritten using diameter as:
$$V = \pi \left( \frac{d}{2} \right)^2 L + \frac{4}{3}\pi \left( \frac{d}{2} \right)^3$$
This formula accurately calculates the volume of a horizontal capsule tank based on its diameter and the length of its cylindrical section.
Vertical capsule tank
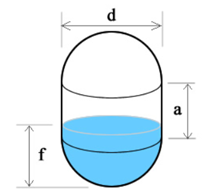
While the volume of filled liquid for this tank will be different from the corresponding filled volume of the horizontal capsule tank, the total volume formula is the same:
V = πr² × ((4/3)r + a) = π × (d/2)² × ((4d/6) + a)
Horizontal elliptical tank with 2:1 semi-elliptical tank heads
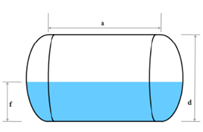
This tank has semi-elliptical heads, with the ellipse's width being twice as long as its depth. If the straight length is a, then the depth of the head, let's denote it as H, will be a/4. Then the total volume of the tank heads can be calculated as follows:
Vₕ = πHd²/3
And the cylinder volume can be calculated as:
V꜀ = (π × d² × a)/4
The total tank volume will be:
V = Vₕ + V꜀
Horizontal tank with dish ends
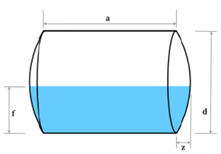
The calculator on this page will also find a horizontal tank's total and filled volume with dish ends. However, the calculation formulas are extensive, and we will not show them here.
Calculation example
An oil tank has a horizontal oval shape, a height of 3 meters, a width of 4 meters, and a length of 6 meters. The manual instructs that this tank cannot be filled above 90% of its total volume. What is the total volume of the tank? If you fill the tank up to the 2.5 meters depth, will you stay within the safe limits?
Let's use the calculator to find out the answers! First, choose "Horizontal Oval" from the drop-down menu. Then enter the known values:
- h = 3
- w = 4
- l = 6
- f = 2.5
After pressing "Calculate" we will see that the total tank volume is ≈ 60.4115 cubic meters or 15,959.03 U.S. gallons. We will also see that filling the tank up to the 2.5 meters depth will result in a fullness of 87.3%, which means you will stay within the safe limits.