Volume Calculator

Every solid three-dimensional object occupies some space. One can think of the space our cell phone occupies when placed on the table, a water storage container placed in the neighborhood, or simply a football on a court.

We can define volume as the space occupied by an object. Volume can also refer to the capacity of the object. Instead of thinking of the space the water container occupies in our garage, we can think of the capacity or the amount of water the container can store.

Volume calculation is used in various disciplines of science and mathematics.

The volume calculator supports multiple measurements when calculating volume. Moreover, the calculator shows the formula and a step-by-step calculation process. This article will provide a simple but sufficient explanation of the volume and volume formula calculator with real examples.

Units and Measurements

To improve the reliability and accuracy of our judgment, we need a standard unit of measurement. For uniformity, we require a standardized set of measurement units, known as standard units.

The SI (International System of Units) volume unit is cubic meter m³. However, some small objects' volumes can be written in smaller units, such as cubic centimeters cm³ or cubic millimeters mm³ if the object is too small.

On the other hand, the user is free to specify the unit that best fits their application. The volume calculator supports two measurement systems: the Metric System, the Imperial and US Customary Units. The user has the freedom to choose between the following units:

• kilometers,
• meters,
• centimeters,
• millimeters,
• micrometers,
• nanometers,
• angstroms,
• miles,
• yards,
• feet,
• inches.

If we use formulas to calculate volume, we must work with a homogeneous units of measure. Therefore, we usually convert all measurements to the same unit to make calculations easier.

For example, consider calculating the volume of a cylinder with a height of 75 cm and a radius of 0.5 m. We either convert the height to meters and calculate the volume in cubic meters or convert the radius to centimeters and find the volume in cubic centimeters.

How about letting you define the height in inches and the radius in nanometers? The calculator will perform even this unit conversion and show the steps.

With this calculator, the user can choose a different unit for each measurement input, and the volume formula calculator will return the volume.

Consider the example where the height of the cylinder is 5 inches and the radius is 10506070 nanometers. We will navigate to the cylinder volume calculator section and input the radius and height values with the correct units from the dropdown list.

The calculator first returns the volume 2.6874044006564 inches³ (in cubic inches) and 4.4038667907438E+22 nanometers³ (cubic nanometers). Why is that? Because these are the measurement units we used in our input, the calculator assumes that we need the volume to be calculated with one of these units. The cylinder volume shows the two ways to conduct the calculation along with the unit conversion!

The Volume Calculator: Scope, Features, and Examples

The methods for calculating volumes can vary from one figure to another. Some geometric shapes use standard arithmetic formulas to calculate their volume based on their properties, such as edge length or radius.

Other geometric shapes are more complex, and you cannot calculate their volume directly. In this case, advanced computational methods such as geometrical integration and finite element methods are used. The volume calculator supports a wide range of objects to compute their volume.

Sphere

A sphere is the three-dimensional equivalent of a circle; an example of a sphere is any round ball (baseball, basketball, etc.). The volume formula of a sphere is given as:

$$V_{sphere}=\frac{4}{3}π r^3$$

We can observe that the volume of a sphere depends only on the sphere's radius (r). The radius is defined as the distance between the center of the sphere and any point on the surface. Given that a baseball has a radius r = 3.65 cm, we can use the volume of a sphere calculator to find the volume:

$$Volume = \frac{4}{3}πr^3 = \frac{4}{3} × π × 3.65^3 = 203.68882488692 \ centimeters^3$$

Cone

A cone is a geometric shape consisting of a circular base and a vertex point, denoted as the apex, where all the base circumference points are connected to the apex with line segments. We can define the cone's properties with two measurements: the circular base's radius (r) and the height between the center of the base center and the apex (h).

A cone's volume can be expressed as:

$$V_{cone}=\frac{1}{3}{π r}^2h$$

r is the radius, and h is the height of the cone

Let's say you have a birthday party and want to do DIY cone-shaped party hats that will then be used as popcorn cones later during the night.

If you decide to do cone hats with a radius of 7.5 cm and a height of 0.45 m, you can use the cone volume calculator to calculate the volume of each cone hat.

0.45 meters = 45 centimeters

$$Volume = \frac{1}{3}πr^2h = \frac{1}{3} × π × 7.52^2 × 45 = 2650.7188014664 \ centimeters^3$$

This means you can put this much popcorn in your cone at the end of the party.

Cube

Who did not have the chance to play with a Rubik's Cube?

This is a geometrical object with 8 vertices and 6 equal sides. A cube's volume only depends on the length of the cube's side (a).

$$V_{cube}=a^3$$

We decided to buy 30 Rubik's cubes for our developmental center so that children could improve their cognitive abilities. We went to the store and found the right cubes for the design and price. The length of the side of the cube is 5.7 centimeters. Unfortunately, the salesman at the store has only one box to stack all the cubes for easy transportation. The box is cubic with 20 centimeters side length. Will all of our cubes fit in that box?

The volume of the cubes:

$$Volume = 5.7³ = 185.19\ centimeters³$$

The total volume of 30 cubes would be

$$185.19 × 30 = 5,555.7\ centimeters³$$

The volume of the box:

$$Volume = 20³ = 8,000\ centimeters³$$

We compared the volume of the 30 cubes to the box's volume.

$$5,555.7 < 8,000$$

And it turned out that the cubes would fit perfectly in the box.

Cylinder

A cylinder is a geometrical prism with a uniform circular base as if multiple circles are placed on top of each other to form this geometrical shape. Like the cone, cylinder properties are defined by the circle's radius (r) and the height from the bottom surface to the top surface of the cylinder (h). One can express the volume of a cylinder as:

$$V_{cylinder}=π r^2h$$

Let's calculate the volume of a decorative cylindrical candle so that the craftsman can understand how much paraffin they will need to make it. So, the height of our candle will be 15 centimeters and the diameter 8 centimeters. From the diameter, we can calculate the radius, which will be 4 centimeters. So we end up with:

$$Volume = πr^2h = π × 4^2 × 15 = 240π = 753.98223686155\ centimeters^3$$

Rectangular Tank

A rectangular tank is a cube variation where all edges are perpendicular but not necessarily equal. This geometrical object is defined by a length (l) and width (w), which represent a two-dimensional rectangle, along with a height (h) that creates this three-dimensional extension of the rectangle. Thus, the volume of the rectangular tank can be written as follows:

$$V_{rectangular\ tank}=l × w × h$$

A universal example of a rectangular tank is the shipping container. The standard shipping container ISO measurements are:

• Width = 2.43 m
• Height = 2.59 m
• Length = 6.06 m or 12.2 m

Since the measurements are standard according to ISO, the volumes are also standard. Go ahead and plug the measurements into the volume of the rectangle tank calculator to find the volume. Perform the calculations for both length values, 6.06 m and 12.2 m.

$$Volume = 6.06 × 2.43 × 2.59 = 38.139822\ meters³$$

and

$$Volume = 12.2 × 2.43 × 2.59 = 76.78314\ meters³$$

More complex three-dimensional geometric shapes

We can combine other geometrical shapes with basic geometrical shapes. What is the volume of this figure?

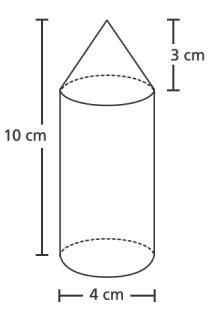
We can see that the object is made up of a cylinder and a cone on top. Therefore, we can say that the volume of the object is the sum of the volume of the cylinder and the volume of the cone:

$$V_{object}=V_{cylinder}+V_{cone}$$

Both the cylinder and the cone have a diameter of 4 cm. Thus, we can say that

$$r_{cylinder}=r_{cone}=\frac{4}{2}=2\ cm$$

Moreover,

$$h_{object}=h_{cylinder}+h_{cone}$$

Given that

$$h_{object}=10\ cm$$

and

$$h_{cone}=3\ cm$$

we can interpret that

$$h_{cylinder}=7\ cm$$

We can now plug the values into the volume calculator as follows:

$$V_{object}=V_{cylinder}+V_{cone}=87.96\ cm^3+12.56\ cm^3$$

$$V_{object}=100.52\ cm^3$$

This example will help better understand the upcoming geometrical shapes that the volume calculator supports.

Capsule

The capsule is one of the most common forms of medical pills. The user can use the previous example to understand that a capsule consists of a cylinder with two hemispheres on two opposite surfaces.

The two hemispheres can add up to a single sphere, and we can say that the volume of a capsule is the sum of the volume of a cylinder and the volume of a sphere.

$$V_{capsule} = πr^2h + \frac{4}{3}πr^3 = πr^2(\frac{4}{3}r + h)$$

Where r is the radius and h is the height of the cylindrical portion.

Thanks to the capsule volume calculator, you do not have to calculate the volume of the cylinder and add it up to that of the sphere to calculate the volume of the capsule. The user can directly input the height and radius, and the calculator will output the volume of the capsule.

Pharmaceutical scientists who analyze, develop, and manufacture medicine always try to find good volumes of capsules. The capsule should store the amount of medication required per capsule, so scientists vary the capsule's dimensions (height and radius) to adjust the volume accordingly.

Spherical Cap

The previous example referred to the hemisphere as half a sphere. Meanwhile, a spherical cap is a portion of the sphere when the sphere is cut by a plane. The hemisphere is a special case of a spherical cap where the sphere is divided into two equal portions. Thus, the volume of a hemisphere is half the volume of a sphere.

The figure below shows an example of a spherical cap where (r) is the radius of the base, (R) is the radius of the sphere and (h) is the height of the spherical cap. There is a relationship between these variables. Thus, it is enough to know two of these values to calculate the third.

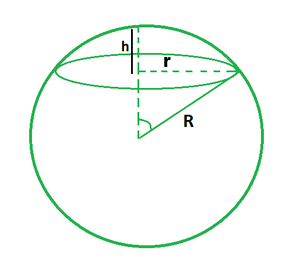
• Given r and R; $h=R±\sqrt{R^2+r^2}$
• Given r and h; $R=\frac{h^2+r^2}{2h}$
• Given R and h; $r=\sqrt{2Rh\ -h^2}$

where:

• r is the radius of the base,
• R is the radius of the sphere,
• h is the height of the spherical cap.

The volume of a spherical cap can be written as follows:

$$V_{spherical\ cap}=\frac{1}{3}π h^2(3R-h)$$

It is enough to enter two of the three variables of the spherical cap. For example, consider that R = 1m and r = 0.25m, the calculator finds two possible volumes; 0.00313 m³ and 4.1856 m³. Why is that?

Recalling the following

$$h=R±\sqrt{R^2+r^2}$$

we can see that when given the values of r and r, h can have two values

$$h_1=R+\sqrt{R^2+r^2}$$

and

$$h_2=R-\sqrt{R^2+r^2}$$

This explains having a different volume value when using $h_1$ and $h_2$.

Besides, the inequality R ≥ r should always hold, or the calculator will return an error message saying, "base radius cannot be larger than ball radius." This error is helpful if the user mixes the values R and r.

Conical Frustum

We can obtain this shape by slicing a cone with a horizontal cut parallel to its circular surface. This results in two circular and two parallel surfaces.

A conical frustum volume can be defined as:

$$V_{conical\ frustum}=\frac{1}{3}π h(r^2+rR+R^2)$$

Where h is the height between the center of the bottom and top surfaces, r is the top surface radius, and R is the bottom surface radius such that R ≥ r.

Imagine you went to a pastry place and saw a lava cake saying that it contained 35% melted chocolate.

If you were a real mathematics enthusiast and would like to translate this into a mathematical problem, you might be interested in the volume of chocolate inside your cake. Well, measure the top and bottom radius along with the height to calculate the volume of the whole cake.

Suppose the measurements are r = 16 cm, R = 20 cm, and h = 10 cm.

Then we can find the cake volume by simply plugging the values in the conical frustum volume calculator.

$$Volume=\frac{1}{3}π h(r^2+rR+R^2)=\frac{1}{3}π 10(16^2+16×20+20^2)= 10220.648099679 \ centimeters^3$$

Besides, 35% of 10,220.65 cm³ is around 3,577.23 cm³ of chocolate.

Ellipsoid

When a sphere is deformed by directional scaling, it produces a surface known as an ellipsoid. One can think of an ellipsoid as a stretched sphere where the distances between the center of the ellipsoid and different points on the surface are not equal.

Thus, the ellipsoid has three axes, and the volume of the ellipsoid is defined relative to the radius from the center to each of these axes. The three radii values are denoted by a, b, and c.

We always think of round spheres whenever we talk about balls, but ellipsoidal balls also exist! Look at the rugby ball. Assume that the dimensions are a = 9.3 cm, b = 9.3 cm, and c = 14.3 cm.

The volume of an ellipsoid is given as:

$$V_{ellipsoid}=\frac{4}{3}π abc$$

The order of a, b, and c is unimportant; mixing them up is okay.

Using the ellipsoid volume calculator, we can get the volume of our rugby ball.

$$Volume=\frac{4}{3}π abc=\frac{4}{3}× π × 9.3 × 9.3 × 14.3 = 5180.7250468112 \ centimeters^3$$

Square Pyramid

Mentioning pyramids might make you think of the ancient pyramids of Egypt. A square pyramid consists of a square base with an apex where the points on the circumference of the base square are connected to that apex. The volume can be calculated as:

$$V_{squared\ pyramid}=\frac{1}{3}a^2h$$

With a being the edge of the square base and h being the height from the square base center to the apex.

We take the dimensions of the Khufu pyramid as it was built originally; h = 146.6 m and a = 230.33 m. The volume of the Khufu pyramid can be calculated as follows:

$$Volume=\frac{1}{3}a^2h = \frac{1}{3}230.33^2 × 146.6 = 2,592,469.9482467\ meters^3$$

Tube

Unlike a cylinder, a tube has an outer and inner diameter. Thus, the tube volume must account for the difference in diameters.

$$V_{tube}=π\frac{d_1^2-d_2^2}{4}l$$

As you have already guessed, d₁ and d₂ are the outer and inner diameters of the tube, respectively. l is the length of the tube.

Let's use the formula to calculate the volume of the concrete ring for the well we're going to dig on our cottage property. The height of our ring is 0.89 meters, the outer diameter is 1.16 meters, and the inner diameter is 1 meter.

So we have the following calculation:

$$Volume=π\frac{1.16^2-1^2}{4} × 0.89 = 0.076896 π = 0.24\ meters^3$$