Distance Calculator

The calculators below can be used to find the distance between two points in a two-dimensional space (2D plane) or three-dimensional space (3D space), as well as to calculate the distance between two places defined with latitude and longitude, or indicated as the points on the world map. There are 3 calculators on this page:

• 2D Distance Calculator
• 3D Distance Calculator
• Distance Between Coordinates Calculator

The 2D Distance Calculator can also be used to determine the line equation and to find the slope and the angle of the line connecting two given points.

Directions for use

2D Distance Calculator

This calculator finds the distance between two points on a 2D plane: point 1 with coordinates (X₁, Y₁) and point 2 with coordinates (X₂, Y₂). To find the distance between two points on a plane, enter the coordinates of both points (X₁, Y₁, X₂, Y₂) into the corresponding fields and press “Calculate.”

The calculator will return the final answer, the detailed solution algorithm, and the graphical representation of the points on the coordinate plane. Additionally, the calculator will find the slope and the angle of the line connecting the two given points and determine the corresponding line equation.

3D Distance Calculator.

This calculator finds the distance between two points in a 3D space: point 1 with coordinates (X₁, Y₁, Z₁) and point 2 with coordinates (X₂, Y₂, Z₂). To calculate the distance between two points in a 3D space, enter the coordinates of both points (X₁, Y₁, Z₁, X₂, Y₂, Z₂) into the corresponding fields, and press “Calculate.” The calculator will return the final answer and the detailed solution algorithm. To empty all fields, press “Clear.”

Distance Between Coordinates Calculator - Distance Based on Latitude and Longitude

Use this calculator to find the distance between two points on the surface of the Earth if their coordinates (latitude and longitude) are known. The calculator finds the distance between point 1 with Latitude 1 and Longitude 1, and point 2 with Latitude 2 and Longitude 2, based on the assumption that the shape of the Earth can be approximated as an ellipsoid. Lambert’s formulas are used for the calculations.

To use this calculator, enter the given values of Latitude 1, Longitude 1, Latitude 2, and Longitude 2 into the corresponding fields, and press “Calculate.” The calculator will return the distance between the points in kilometers and miles.

Input values

The coordinates can be entered as follows:

• Degree-minute-second format, followed by a compass direction from the drop-down menus – N(orth) or S(outh) for Latitude, and E(ast) or W(est) for Longitude. Here, Latitudes should be represented by values between -90 and 90, and values between -180 and 180 should represent Longitudes.
• Decimals without a compass direction. The sign of the values then represents the direction: Latitude is positive in the North (of the equator), negative in the South, and Longitude is positive in the East (of the Prime Meridian) and negative in the West. Also, here, Latitudes should be represented by values between -90 and 90, and values between -180 and 180 should represent Longitudes. To empty all fields, press “Clear.”

Distance Between Two Points on the Map Calculator

This calculator also finds the distance between two points on the surface of the Earth based on the assumption that the shape of the Earth can be approximated as an ellipsoid and uses Lambert’s formulas for the calculations.

To use this calculator, select two points on the provided map. The calculator will automatically determine the (decimal) coordinates of the selected points and calculate the distance in kilometers and miles.

All calculators accept integers, decimals, and numbers in e-notation as inputs.

Formulas

In all formulas presented below, distance is indicated as d.

2D distance formula

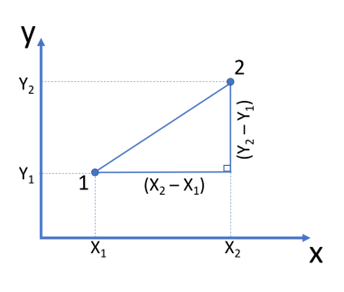
The distance between two points with coordinates (X₁, Y₁) and (X₂, Y₂) on a two-dimensional plane is calculated with the help of the Pythagorean theorem by the following formula:

$$d=\sqrt{(X₂ - X₁)²+(Y₂ - Y₁)²}$$

3D distance formula

The above formula can be extrapolated into 3 dimensions to find the distance between point 1 with coordinates (X₁, Y₁, Z₁) and point 2 with coordinates (X₂, Y₂, Z₂) as follows:

$$d=\sqrt{(X₂ - X₁)²+(Y₂ - Y₁)²+(Z₂ - Z₁)²}$$

Calculating distance based on latitude and longitude

This section will use the following symbols: ϕ for latitude and λ for longitude. A point with Latitude 1 and Longitude 1 will be described as (ϕ1, λ1).

To calculate the distance between two points on the surface of the Earth, we need to calculate the distance along the Earth’s surface. Therefore, we have to choose an approximation for the shape of the Earth’s surface. There are three most common approximations:

1. Flat surface. This approximation works quite well for short distances. The 2D distance formula can be used in this case. Several further approximations exist to account for the variation in distance between meridians when projecting the Earth’s surface onto a plane.
2. Spherical surface. The formula for this approximation is based on the assumption that the Earth’s surface can be approximated as a sphere. Spherical trigonometry is then used to derive a more precise formula that can be used for considerable distances with an accuracy of about 5%. This formula is called the great-circle distance formula, or the haversine formula, because it was derived with the help of a haversine – a special trigonometric function. A haversine of angle θ is defined as follows: \$hav\ θ=\frac{(1-cos⁡θ)}{2}\$. And the haversine formula for distance between two points with coordinates (ϕ₁, λ₁) and (ϕ₂, λ₂) looks like this:

$$d=2r\ arcsin\sqrt{hav(φ₂-φ₁ )+(1-hav(φ₁-φ₂ )-hav(φ₁+φ₂ ))× hav(λ₂-λ₁)}$$

$$d=2r\ arcsin\left( \sqrt{(sin²\left( \frac{φ₂-φ₁}{2} \right)⁡+cos⁡\ φ₁×cos⁡\ φ₂ × sin²\left( \frac{λ₂-λ₁}{2} \right)⁡}\right)$$

Where r – is the radius of the sphere under investigation (in our case, the average radius of the Earth).

3. Ellipsoidal surface. This approximation is the most precise since the actual shape of the Earth is closer to an ellipsoid than to a sphere. The shortest line (path) connecting the two points on the surface of an ellipsoid is called the geodesic, and the length of that path is calculated with Lambert’s formulas. These formulas use reduced latitudes β₁ and β₂ instead of ϕ₁ and ϕ₂: tan β = (1 - f) × tan ϕ, where f – is the flattening. The distance is found as follows:

d = a (σ – f/2(X + Y))

Where a – is the equatorial radius of the ellipsoid (in our case, the Earth), σ – is the central angle between point 1 (β₁, λ₁) and point 2 (β₂, λ₂) in radians. This angle is calculated using the haversine formula described above, assuming that longitudes are the same on a sphere and a corresponding ellipsoid. X and Y are calculated using the following formulas:

$$X=(σ-sin⁡σ)\frac{sin²⁡P\ cos²⁡Q}{cos²\frac{σ}{2}⁡}$$

$$Y=(σ-sin⁡σ)\frac{cos²⁡P\ sin²⁡Q}{sin²\frac{σ}{2}⁡}$$

where, P = (β₁ + β₂)/2 and Q = (β₂ – β₁)/2

Real-life applications

Usually, we mean 2D or 3D distance when we talk about distance. This includes various examples:

• The distance between the queue's end and the line's front (for a straight-line queue).
• The length of the slope of the hill where you are skiing.
• Even the distance between the sun and the planets of the solar system.

The latitude and longitude distance, or the distance between the points on the map, is very often used to calculate the flight path of an airplane travelling from point A to point B since a plane flying from one place to another is going along the ellipsoidal surface of the Earth – precisely the situation described by Lambert’s formulas!