Distance Formula Calculator

This calculator finds the distance between two points on a plane if the coordinates of the points are known. The calculator operates in a two-dimensional space.

Since a straight line represents the shortest distance between 2 points, this calculator can be used as a line length calculator.

Directions for use

The calculator finds the distance between point 1 with coordinates (X₁, Y₁) and point 2 with coordinates (X₂, Y₂).

To find the distance between two points, enter their coordinates into the corresponding fields. The input coordinates should be entered as follows:

• A comma should separate two coordinates of each point; for example, enter “4,5” into the (X₁, Y₁) field to have point 1 with the x-coordinate of 4 and a y-coordinate of 5. If any of the coordinates is represented by a decimal, use the decimal point to separate the whole number part from the decimal part; for example, enter “4.5,7” to have a point with an x-coordinate of 4.5 and a y-coordinate of 7.
• You can only use integers and decimals as point coordinates. Fractions are not accepted.
• Spaces between the coordinates are not necessary, but you can use them for your convenience

After entering the coordinates, press “Calculate.” The calculator will return the final answer and the detailed solution algorithm.

Distance formula

On a two-dimensional plane, the distance d between point 1 with coordinates (X₁, Y₁) and point 2 with coordinates (X₂, Y₂) can be found with the help of the following formula:

$$d=\sqrt{(X₂-X₁)^2+(Y₂-Y₁)^2}$$

Or, in other words: the distance between 2 points in a 2-dimensional space can be found as the square root of the sum of squared differences of the corresponding coordinates. This formula is known as the Euclidean distance formula. Therefore, this calculator can also be called a Euclidean distance calculator.

Euclidean distance formula derivation

To derive the formula, let’s look at the two given points on the (X, Y) coordinate plane:

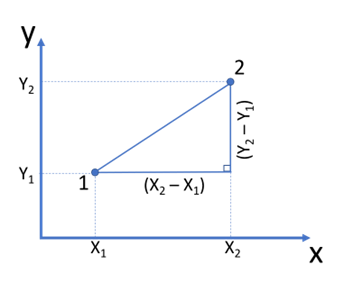
To find the distance between point 1 and point 2, let’s draw a vertical line down from point 2, and a horizontal line to the right from point 1. The two drawn lines and the necessary distance will form a right triangle. The vertical leg of this triangle will be formed by the vertical distance between point 1 and point 2: Y₂ – Y₁. The horizontal leg of the triangle will be formed by the horizontal distance between the two points: X₂ – X₁. The hypotenuse of this triangle represents the necessary distance between the points. When the lengths of the legs of the right triangle are known, the length of the hypotenuse can be found with the help of the Pythagorean theorem:

$$d^2=(X₂-X₁)^2+(Y₂-Y₁)^2$$

$$d=\sqrt{(X₂-X₁)^2+(Y₂-Y₁)^2}$$

Calculation examples

Example 1

Let’s find the distance between point 1 with (X₁, Y₁) = (3, 1) and point 2 with (X₂, Y₂) = (5, 7). Substituting the values of X₁, Y₁, X₂, Y₂ in the Euclidean distance formula, we will get:

$$d=\sqrt{(X₂-X₁)^2+(Y₂-Y₁)^2}=\sqrt{(5-3)^2+(7-1)^2}=\sqrt{2^2+6^2}$$

$$\sqrt{2^2+6^2}=\sqrt{4+36}=\sqrt{40}=2\sqrt{10}\approx 6.32$$

Note that changing the order of the points does not change the final result since the differences between the coordinates are squared. Let’s repeat the above calculation, assuming that (X₁, Y₁) = (5, 7), and (X₂, Y₂) = (3, 1):

$$d=\sqrt{(X₂-X₁)^2+(Y₂-Y₁)^2}=\sqrt{(3-5)^2+(1-7)^2}=\sqrt{-2^2+-6^2}$$

$$\sqrt{2^2+6^2}=\sqrt{4+36}=\sqrt{40}=2\sqrt{10}\approx 6.32$$

Example 2

Let’s look at an example with negative coordinates and find the distance between point 1 with (X₁, Y₁) = (-4, 2) and point 2 with (X₂, Y₂) = (6, -6). Substituting the values of X₁, Y₁, X₂, Y₂ in the Euclidean distance formula, we will get:

$$d=\sqrt{(X₂-X₁)^2+(Y₂-Y₁)^2}=\sqrt{(6-(-4))^2+(-6-2)^2}=\sqrt{10^2+(-8)^2}$$

$$\sqrt{10^2+(-8)^2}=\sqrt{100+64}=\sqrt{164}=2\sqrt{41}\approx 12.8$$

Real-life examples

As shown above, the Euclidean distance formula is based on the Pythagorean theorem. Still, it adapts the theorem to situations where only the coordinates of the points are known (rather than the lengths of the sides of the triangle used by the Pythagorean theorem). The formula is useful when distances must be calculated from the coordinates on a map or graph. It is also used to calculate magnitudes of complex numbers and vectors.

Example 3

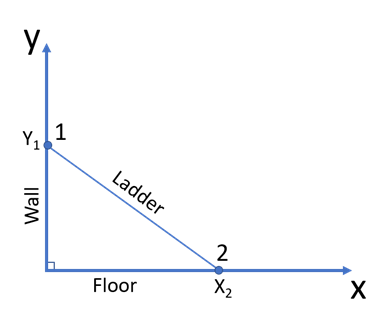
Imagine a ladder leaning against the wall. In this situation, the floor represents the x-axis of the 2D plane, and the wall represents the y-axis, as shown in the image below. If the ladder touches the wall at point (0, 2), and touches the floor at point (3, 0), find the length of the ladder.

Solution

To find the length of the ladder in a 2-dimensional plane formed by the wall and the floor, let’s first identify the coordinates of the endpoints of the ladder: X₁, Y₁, X₂, Y₂. Let’s call the point where the ladder touches the wall – point 1 (X₁, Y₁), and the point where the ladder touches the floor – point 2 (X₂, Y₂). We know that the ladder touches the wall at the point with the coordinates (0, 2). Therefore, (X₁, Y₁) = (0, 2):

X₁ = 0, Y₁ = 2

Note how X₁ = 0, which is clearly illustrated by the above image, where point (0, 0) corresponds to the physical point where the wall meets the floor, making negative values of X and Y impossible.

Furthermore, we know that the ladder touches the floor at the point with the coordinates (3, 0). Therefore, (X₂, Y₂) = (3, 0):

X₂ = 3, Y₂ = 0

Also, Y₂ = 0 since these coordinates correspond to the point directly on the floor. Now let’s use the distance formula to calculate the length of the ladder:

$$d=\sqrt{(X₂-X₁)^2+(Y₂-Y₁)^2}=\sqrt{(3-0)^2+(0-2)^2}=\sqrt{3^2+(-2)^2}$$

$$\sqrt{3^2+(-2)^2}=\sqrt{9+4}=\sqrt{13}\approx 3.6$$

Answer

The length of the ladder is 3.6.

Distance in 3D-space

Euclidean distance is what most people refer to as “distance.” When we say an object is 5 meters away from us, it’s the Euclidean distance we have in mind. The distance formula described above can be easily extrapolated into 3 (or even more!) dimensions.

In a 3-dimensional space, the distance between point 1 with coordinates (X₁, Y₁, Z₁) and point 2 with coordinates (X₂, Y₂, Z₂) can be calculated as the square root of the sum of the squared differences between the corresponding coordinates:

$$d=\sqrt{(X₂-X₁)^2+(Y₂-Y₁)^2+(Z₂-Z₁)^2}$$