Fraction to Decimal Calculator

The fraction to decimal calculator is an online and free calculator to convert fractions to decimals. We can perform fractions to decimals conversions manually using several methods such as long division. However, this easy-to-use calculator performs the conversion quickly.

The user can find the equivalent of any fraction by just plugging in the values of the numerator and denominator, specifying the rounding options, and pressing calculate! The tool also shows the calculation steps taken to perform the conversion. The following sections will explain fractions, decimals, and rounding to equip the user with the important information to use this tool effectively.

By definition, fractions are numerical quantities representing a part or proportion of something. From a mathematical point of view, a fraction defines a part of a whole. The word “whole” can represent a number, a quantity, or even a pizza or a pie!

Looking at the picture below, one can say that one-eighth of the pizza is missing, or \$\frac{1}{8}\$ of the pizza is missing. How is this inference obtained? First, let us count the total number of slices a “whole” pizza is composed of. This is 8 slices.

This brings us to say that \$\frac{1}{8}\$ of the pizza is gone or \$\frac{7}{8}\$ of the pizza is left.

A fraction consists of two parts; a numerator representing the number above the fractional bar and a denominator, the number below the fraction bar. Fractions can be positive or negative.

Fractions types

There are several types of fractions according to their different properties. Some of them are listed below:

Proper Fractions

Are fractions where the denominator is greater than the numerator. Examples:

$$\frac{10}{11},\frac{5}{7},\frac{999}{1000}$$

Improper Fractions

Improper fractions are fractions where the numerator (the top number) is equal to or greater than the denominator (the bottom number). This means that the value of the fraction is equal to or greater than 1.

Examples:

$$\frac{5}{4},\frac{8}{7},\frac{567}{123}$$

Mixed Fractions

Are fractions consisting of a whole number with a proper fraction. In the previous example, we were able to write the improper fraction \$\frac{5}{4}\$ as a mixed fraction \$1\frac{1}{4}\$ where 1 is the whole number and \$\frac{1}{4}\$ is the proper fraction.

Unit Fractions

Are fractions with a numerator with value of 1. An example can be \$\frac{1}{4}\$ or \$\frac{1}{1254}\$

Decimals

A decimal number is a number which integer and fractional parts are separated by a decimal point.

Looking at the two equivalent fractions \$\frac{5}{4}\$ and \$1\frac{1}{4}\$, we can transform fraction into decimal using the fraction to decimal calculator and write it as \$\frac{5}{4}=1\frac{1}{4}=1.25\$.

Just like fractions, decimal numbers can also be positive or negative. We distinguish two major types of decimal numbers:

Terminating Decimal Numbers

These are decimal numbers with a finite number of digits after the decimal point. This means that the digits after the decimal point are countable, and such decimal numbers can be called exact decimal numbers, such as 1.23 or 7.7894512554.

Non-Terminating Decimal Numbers

These are decimal numbers with an infinite number of digits after the decimal point. We can also separate non-terminating decimal numbers into two classes: recurring and non-recurring decimal numbers.

Recurring Decimal Numbers

The numbers after the decimal point are repetitive in the same pattern, such as 5.141414… where the value “14” is always repeating.

Non-Recurring Decimal Numbers

Non-recurring decimal numbers are decimal numbers where the digits after the decimal point do not repeat in any pattern. These numbers can be either finite or infinite in length. Finite non-recurring decimals have a limited number of digits after the decimal point and end without forming any repetitive sequence. An example of a finite non-recurring decimal is 0.123, which has three unique digits after the decimal point and then terminates.

Infinite non-recurring decimals, on the other hand, continue indefinitely without repeating a pattern. A well-known example is the mathematical constant π (approximately 3.14159), which extends infinitely with no repeating sequence of digits. These types of decimals are essential in representing precise measurements and irrational numbers in mathematics.

Manual conversion of fraction to decimal

1. Convert the denominator to 10, 100, or 1,000

This method is very simple, but it does not work for every fraction.

First, multiply the numerator and denominator by a number that converts the bottom of the fraction to 10 or 100, 1000, and so on.

Let's say we need to convert a fraction with a numerator of 6 and a denominator of 25. We can get 100 at the bottom just by multiplying 25 by 4. Don't forget to multiply the upper part. So, we get 24.

$$\frac{6}{25}=\frac{6 × 4}{25 × 4}= \frac{24}{100}$$

Write down the numerator separately. Count from the right the number of digits you got in the denominator after multiplication (3 digits in 100), and put a comma on that position. This will be the decimal you are looking for - 0.24.

Another example:

$$\frac{13}{40}=\frac{13 × 25}{40 × 25}= \frac{325}{1000}=0.325$$

The current method is unsuitable if you cannot find such a multiplier that can convert the denominator into 10, 100, or 1000. In that case use the second method.

2. Divide the numerator by the denominator

To convert a fraction into a decimal, divide the upper part of the fraction by the lower part. Of course, the easiest way to do this is with a calculator.

If it is important for you to do without any devices, use the manual division method. For example, convert a fraction with a numerator of 80 and a denominator of 125. By manually dividing 80 by 125, we get 0.64.

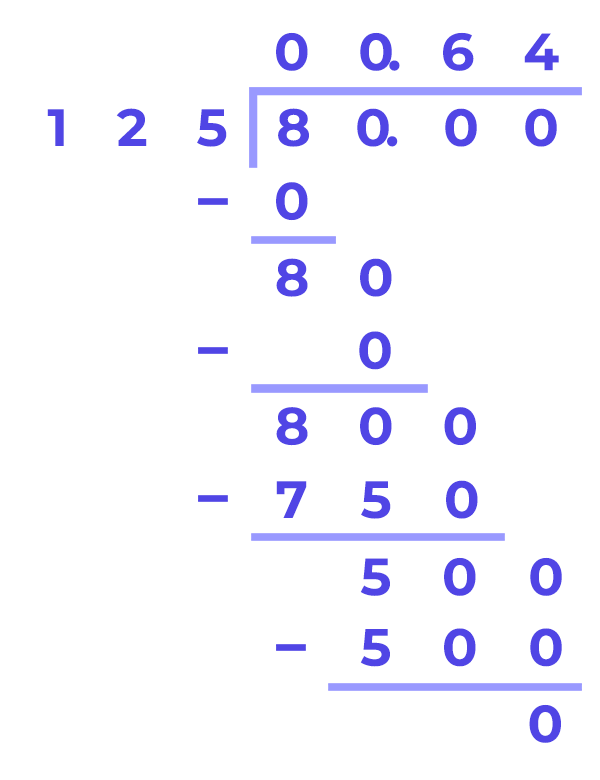
Suppose, when dividing manually, you realize that the process does not end and repeated digits line up after the comma. In that case, this fraction cannot be converted to a terminating decimal.

The answer can be written as non-terminating decimal. To do this, write the repeating digits in parentheses, like this: \$\frac{2}{3}=0.6666... = 0.(6)\$ or \$\frac{7}{6}= 1.6666... = 1.(6)\$ or \$\frac{6}{22}=0.272727... = 0.(27)\$

A fraction \$\frac{a}{b}\$ can be converted into a terminating decimal number only if the decomposition of the denominator of b into prime factors contains no other numbers except 2 and 5.

Fraction to Decimal Conversion Application

So, why do we need to convert fractions into decimals? Decimals are more interpretable and accurate than fractions. For example, compare the following two fractions:

$$\frac{6458}{749894} \ and \ \frac{8798}{846489}$$

It is not an easy task to compare these two fractions just by looking at them.

Let's use the precision power of decimals. Let's do the conversion with rounding to the nearest millionth:

$$\frac{6458}{749894}=0.008612 \ and \ \frac{8798}{846489}=0.010394$$

Now, we can clearly say that since

$$0.008612 < 0.010394$$

then

$$\frac{6458}{749894} < \frac{8798}{846489}$$

Calculating percentages is one example that illustrates the handy use of fractions in a decimal calculator.

Example 1

Jack arrived at the family meeting. A total of seven people attended the celebration. Jack ordered a bacon pizza to divide it equally among them all. When the pizza was cut, Jack ate 1 slice. That is, he got \$\frac{1}{7}\$ of the pizza.

The next weekend, 13 relatives came to the meeting. So Jack ordered the bacon pizza again. When the pizza was delivered and he cut it into 13 slices, an unforeseen circumstance came to light. He hadn't considered that some of the relatives who had arrived that day were vegetarians and they wouldn't eat the bacon pizza. Jack got lucky and got two slices of his favorite pizza. So he ate \$\frac{2}{13}\$ that day. How do we get to know which time Jack ate more?

To compare these numbers, it will be more convenient to convert the fractions to decimals. At the first home meeting, Jack ate \$\frac{1}{7}=0.1428571428571429\$ of the pizza. At the second home meeting, Jack ate \$\frac{2}{13}=0.1538461538461538461538\$ of the pizza.

$$0.142857141428571429 < 0.1538461538461538$$

or

$$0.14 < 0.15$$

The difference was not that big, but it turns out that Jack got a little more the second time.

Example 2

Consider a class of 83 students, 37 boys and 46 girls. In this class 21 students like literature, 57 like science, and 5 like mathematics.

We can start representing these parts of a whole as fractions. Then, the calculator can convert fractions to decimals (rounding to the nearest hundredth), and we can find percentages by multiplying the result by 100 afterward.

• The percentage of boys in the class:

$$\frac{37}{83} × 100\%≈ 0.45 × 100\% ≈ 45\%$$

• The percentage of girls in the class:

$$\frac{46}{83} × 100\% ≈ 0.55 × 100\% ≈ 55\%$$

We can see that decimal numbers and percentages are more interpretable than fractions. Consequently, we can write the following;

• The percentage of students who like literature:

$$\frac{21}{83} × 100\% ≈ 0.25 × 100\% ≈ 25\%$$

• The percentage of students who like science:

$$\frac{57}{83} × 100\% ≈ 0.69 × 100\% ≈ 69\%$$

• The percentage of students who like mathematics:

$$\frac{5}{83} × 100\% ≈ 0.06 × 100\% ≈ 6\%$$

Related Questions

• What is 5/8 as a decimal?
• What is 1/8 as a decimal?
• What is 1/3 as a decimal?
• What is 7/8 as a decimal?
• What is 2/3 as a decimal?
• What is 3/4 as a decimal?