Equivalent Fractions Calculator

This versatile equivalent fractions calculator quickly finds equivalent fractions for any given fraction, integer, or mixed number. Whether your input values are positive or negative, the tool handles them seamlessly. When working with integers and mixed numbers, the calculator automatically converts them into their fractional forms to generate equivalents. If you enter an existing fraction, you can also use this tool as a highly convenient fraction-to-fraction converter.

Directions for use

Using this calculator is simple: just enter your starting value and click "Calculate" to instantly view a list of equivalent fractions.

Input value limitations

This equivalent fractions finder accepts the following numerical formats:

1. Proper fractions. For example, \$\frac{1}{3}\$ or \$-\frac{16}{32}\$. Note that your fractions do not need to be simplified beforehand.
2. Improper fractions. For example, \$-\frac{5}{2}\$ or \$\frac{16}{8}\$.
3. Mixed numbers. When entering a mixed number, separate the whole number from the fractional part using a single space. For example, \$2\frac{2}{3}\$ or \$5\frac{9}{2}\$. The fractional part of the mixed number can be either proper or improper.
4. Integers, with the exception of zero. For example, 92 or -1.

Definitions

Equivalent fractions are fractions that represent the exact same mathematical value, even though they are made up of different numbers. For example, \$\frac{1}{2}\$ is perfectly equivalent to \$\frac{4}{8}\$ because they both represent a half, despite using different numerators and denominators.

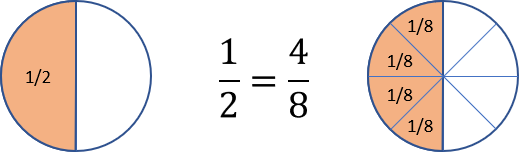
How to find equivalent fractions

To manually find equivalent fractions, simply multiply or divide both the numerator (the top number) and the denominator (the bottom number) of your starting fraction by the same exact value. This mathematical rule works as long as both resulting numbers remain whole integers (no decimals or secondary fractions).

For instance, if you want to generate equivalent fractions for \$\frac{1}{2}\$, you can multiply the top and bottom by ANY whole number.

Let’s calculate some equivalent fractions of \$\frac{1}{2}\$ by repeatedly multiplying by 4:

\$\frac{1}{2}\$ = \$\frac{1 × 4}{2 × 4}\$ = \$\frac{4}{8}\$ = \$\frac{16}{32}\$ = \$\frac{64}{128}\$ …

Because you can multiply these numbers infinitely, every fraction has an endless number of equivalent fractions.

It's also important to note that because we calculate equivalent fractions by multiplying or dividing by the same value, the simplified (or lowest) form of all equivalent fractions will always be identical.

Consequently, two fractions that have entirely different simplest forms can never be equivalent to one another.

Checking if two fractions are equivalent

A reliable way to check if two given fractions are equivalent is to calculate their cross products. If the resulting cross products are equal, the fractions are equivalent.

Example 1

Let’s determine if \$\frac{1}{3}\$ and \$\frac{4}{11}\$ are equivalent. To find the cross products, multiply the numerator of the first fraction by the denominator of the second. Then, multiply the denominator of the first fraction by the numerator of the second:

$$\frac{1}{3}\ and\ \frac{4}{11}$$

The cross products of these two fractions are (1 × 11) = 11 and (3 × 4) = 12. Since 11 ≠ 12, we know that \$\frac{1}{3}\$ ≠ \$\frac{4}{11}\$. Therefore, these fractions are not equivalent.

Example 2

Which fraction is equivalent to \$\frac{2}{3}\$: \$\frac{12}{18}\$ or \$\frac{12}{19}\$?

To solve this, we must compare the cross products for both pairs of fractions:

$$\frac{2}{3}\ and\ \frac{12}{18}$$

$$\frac{2}{3}\ and\ \frac{12}{19}$$

For \$\frac{2}{3}\$ and \$\frac{12}{18}\$, the cross products are (2 × 18) = 36 and (3 × 12) = 36. Because these cross products are equal, \$\frac{2}{3}\$ and \$\frac{12}{18}\$ are equivalent fractions.

For \$\frac{2}{3}\$ and \$\frac{12}{19}\$, the cross products are (2 × 19) = 38 and (3 × 12) = 36. Since 38 ≠ 36, \$\frac{2}{3}\$ and \$\frac{12}{19}\$ are not equivalent.

Calculation example

In practical, everyday scenarios, understanding how to find equivalent fractions is highly beneficial. It allows us to easily add, subtract, or compare fractions that have different denominators, as well as seamlessly blend fractions with mixed numbers or integers.

Cutting the pizza

Let’s look at a relatable example: cutting a pizza. Imagine you and a friend order a pizza, but it arrives entirely uncut. You want to share the pizza equally, but simply cutting it down the middle and holding one massive half isn't very practical. How many slices should you cut the pizza into, and how many slices will each of you get?

Solution 1

Naturally, each person will end up eating exactly half the pizza, represented as \$\frac{1}{2}\$. To figure out better slicing options, we need to find fractions that are equivalent to \$\frac{1}{2}\$. Let’s start by continuously multiplying the numerator and the denominator of \$\frac{1}{2}\$ by 2. We get:

\$\frac{1}{2}\$ = \$\frac{1 × 2}{2 × 2}\$ = \$\frac{2}{4}\$ = \$\frac{4}{8}\$ = \$\frac{8}{16}\$ …

This math tells us you can cut the pizza into 4 slices, allowing each of you to eat 2. Alternatively, you could slice it smaller into 8 slices, with each of you taking 4. You could even cut it into 16 slices, meaning you both get 8. Cutting a standard pizza into more than 16 slices becomes quite messy, so we'll stop our calculations there!

Solution 2

Alternatively, you can uncover different slicing arrangements by multiplying the original fraction by a different progressive whole number each time:

\$\frac{1}{2}\$ = \$\frac{1 × 2}{2 × 2}\$ = \$\frac{2}{4}\$ = \$\frac{1 × 3}{2 × 3}\$ = \$\frac{3}{6}\$ = \$\frac{1 × 4}{2 × 4}\$ = \$\frac{4}{8}\$ = \$\frac{1 × 5}{2 × 5}\$ = \$\frac{5}{10}\$ = \$\frac{1 × 6}{2 × 6}\$ = \$\frac{6}{12}\$ = \$\frac{1 × 7}{2 × 7}\$ = \$\frac{7}{14}\$ = \$\frac{1 × 8}{2 × 8}\$ = \$\frac{8}{16}\$ …

In this approach, some of the resulting equivalent fractions will match the ones we found in Solution 1, but others will be entirely new. We still see \$\frac{2}{4}\$, \$\frac{4}{8}\$, and \$\frac{8}{16}\$, but now we also have the additional options of \$\frac{3}{6}\$, \$\frac{5}{10}\$, \$\frac{6}{12}\$, and \$\frac{7}{14}\$.

Practically, this means you can slice the pizza into 6 pieces (with each of you eating 3), 10 pieces (eating 5 each), or 12 pieces (eating 6 each), and so on. This mathematical sequence can continue indefinitely, but we’re only highlighting the fractions that make sense for a real-world pizza!

Answer

\$\frac{1}{2}\$ = \$\frac{2}{4}\$ = \$\frac{3}{6}\$ = \$\frac{4}{8}\$ = \$\frac{5}{10}\$ = \$\frac{6}{12}\$ = \$\frac{7}{14}\$ = \$\frac{8}{16}\$ …

In all of these equivalent fractions, the denominator represents the total number of pizza slices, while the corresponding numerator represents the exact number of slices each person gets to enjoy.