Fraction to Percent Calculator

This calculator converts given fractions to percentages. You can convert both proper and improper fractions.

Directions for use

To use this fraction to percent converter, enter the numerator and the denominator of the given fraction into the corresponding fields. Choose the number of decimals after the decimal point from the drop-down menu, and press “Calculate.” The calculator will return the final answer, as well as the solution algorithm.

Note, that the drop-down menu for the number of decimals also contains the “Decimals to Round to” option. If you remove any numbers from the input field, the final answer will still be rounded, but up to the 14th decimal.

Note also, that you can use positive and negative inputs for both the numerator and the denominator. If only one of the inputs has a negative sign, the calculator will automatically assign it to the numerator (even if you input it to the denominator field), since \$\frac{-a}{b}\$ = \$\frac{a}{-b}\$ = \$-\frac{a}{b}\$. If both the numerator and the denominator have a negative sign, it will be automatically cancelled, since \$\frac{-a}{-b}\$ = \$\frac{a}{b}\$.

Limitations on the input values

Only integers are accepted as inputs for the numerator and the denominator of the given fraction.

A zero denominator is undefined, therefore, 0 is not a valid input for the denominator (but can be input as the numerator).

Turning fractions into percents

Definitions

Fraction – is a number consisting of two parts, a numerator and a denominator. These two parts are separated by a fraction bar. A fraction represents a part of a whole, where the denominator represents a whole, and the numerator represents the part. \$\frac{3}{5}\$, \$\frac{5}{12}\$, and \$\frac{7}{2}\$ are all fractions. For example, \$\frac{3}{5}\$ means that “the whole” was divided into 5 pieces, and we are only talking about 3 of them.

If the numerator of a fraction is equal to the denominator or is larger than the denominator, the fraction is called improper. If the denominator of a fraction is larger than the numerator, the fraction is called proper.

Percentage – is a number describing a fraction of a hundred. Therefore, a percentage is basically a fraction with 100 as the denominator. The denominator is omitted, and the value is presented as percent, %. For example, \$\frac{30}{100}\$ = 30%, \$\frac{120}{100}\$ = 120%.

Fraction to percent conversion algorithm

To convert a fraction to percentage, you need to follow the steps below:

1. Perform fraction to decimal conversion (by using division).
2. Multiply the result of step 1 by 100, to get the percentage.

The steps above are interchangeable – you can first multiply the numerator by 100, and then divide the obtained result by the denominator.

For example, let’s convert \$\frac{4}{25}\$ to percentage, rounding up to 2 decimals:

1. \$\frac{4}{25}\$ = 4 ÷ 25

Using long division, we get:

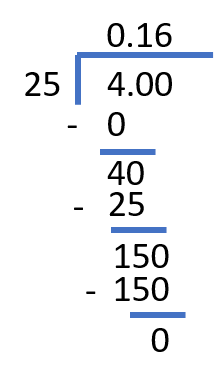
\$\frac{4}{25}\$ = 4 ÷ 25 = 0.16

2. Multiplying by 100, we get:

0.16 × 100 = 16%

Finally, \$\frac{4}{25}\$ = 16%.

Similarly, reversing the steps, we get:

1. 4 × 100 = 400
2. 400 ÷ 25 = 16

4.25 = 16%

Fraction to Percent Conversion Table

The following table provides a detailed conversion of common fractions into their equivalent percentage values.

Each row in the table corresponds to a specific fraction, ranging from simple fractions like 1/2, which converts to 50%, to more complex ones like 1/7, translating to approximately 14.285714%. The table covers a wide range of fractions up to 9/10, presenting their conversion to percentages to aid clarity.

For example, the fraction 1/3 is converted to 33.33%, which illustrates how one part of a three-part whole translates into a percentage. Similarly, the fraction 8/9 equates to 88.888889%, demonstrating what proportion of a whole is represented when eight out of nine parts are considered.

Fraction	Percent
1/2	50 %
1/3	33.33 %
2/3	66.67 %
1/4	25 %
2/4	50 %
3/4	75 %
1/5	20 %
2/5	40 %
3/5	60 %
4/5	80 %
1/6	16.67 %
2/6	33.33 %
3/6	50 %
4/6	66.67 %
5/6	83.33 %
1/7	14.285714 %
2/7	28.571429 %
3/7	42.857143 %
4/7	57.142858 %
5/7	71.428571 %
6/7	85.714286 %
1/8	12.5 %
2/8	25 %
3/8	37.5 %
4/8	50 %
5/8	62.5 %
6/8	75 %
7/8	87.5 %
1/9	11.111111 %
2/9	22.222222 %
3/9	33.333333 %
4/9	44.444444 %
5/9	55.555556 %
6/9	66.666667 %
7/9	77.777778 %
8/9	88.888889 %
1/10	10 %
2/10	20 %
3/10	30 %
4/10	40 %
5/10	50 %
6/10	60 %
7/10	70 %
8/10	80 %
9/10	90 %

This table is a useful tool for anyone who needs to realize how parts of a whole are displayed in a clear percentage format. This simple and systematic table makes it easier to understand data, proportions and ratios in everyday life.

Calculation examples

Reporting survey results

Percentages are very often used to present survey results in a convenient way.

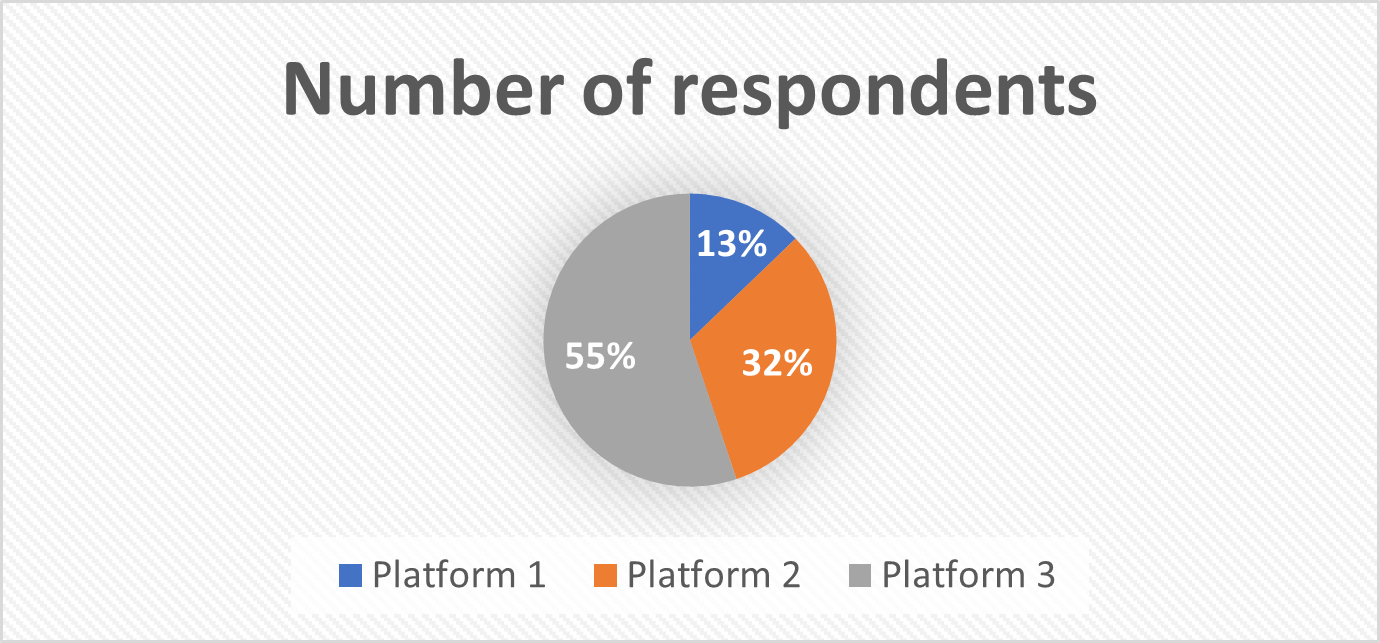
Imagine you made a survey asking people which social media platform they prefer. You have asked 78 people, out of which 10 – preferred Platform 1, 25 – preferred Platform 2, and the rest preferred Platform 3. Present your survey results as percentages rounding up to two decimal points, and draw a pie-chart rounding the results to whole numbers, to visually represent the results.

Solution

You have asked the total of 78 people, therefore, 78 represents your 100%. To present your results in percentages you need to convert the following fractions:

• Platform 1: \$\frac{10}{78}\$
• Platform 2: \$\frac{25}{78}\$
• Platform 3: \$\frac{78 – 25 – 10}{78}\$ = \$\frac{43}{78}\$

Converting \$\frac{10}{78}\$ to percentage:

1. \$\frac{10}{78}\$ = 10 ÷ 78 ≈ 0.1282
2. 0.1282 × 100 = 12.82%

Let’s reverse the steps to convert \$\frac{25}{78}\$ to percentage:

1. 25 × 100 = 2500
2. 2500 ÷ 78 ≈ 32.05%

Converting \$\frac{43}{78}\$ to percentage:

1. 43 × 100 = 4300
2. 4300 ÷ 78 ≈ 55.13%

To check, whether our calculations are correct, we can sum up the acquired percentages, to make sure their sum amounts to 100%:

12.82% + 32.05% + 55.13% = 100%

Converting the results to whole numbers, we get:

12.82% ≈ 13%, 32.05% ≈ 32%, 55.13% ≈ 55%. The chart will look like this:

Answer

12.82% of respondents prefer Platform 1, 32.05% prefer Platform 2, and 55.13% prefer Platform 3.

Earth’s atmosphere

About \$\frac{39}{50}\$ of the atmosphere of Earth consists of nitrogen. What is the percentage of nitrogen in the atmosphere of our planet?

Solution

To figure out the percentage of nitrogen in the atmosphere of Earth, we need to convert the given fraction \$\frac{39}{50}\$ to percentage. Let’s do the conversion by first multiplying the numerator by 100, and then dividing it by the denominator:

1. 39 × 100 = 3900
2. 3900 ÷ 50 = 78

\$\frac{39}{50}\$ = 78%

Answer

Earth’s atmosphere consists of about 78% nitrogen.

Test scores

Jane got her test results for several subjects today. She got a 92% score in Math, and a score of \$\frac{9}{12}\$ in Chemistry. In which discipline does Jane have a better score?

Solution

To compare the two test results, we need to bring them to the same format. Let’s convert \$\frac{9}{12}\$ to percentage. Let’s use the algorithm of converting the number to a decimal, and then converting the decimal to percentage. To make the process slightly easier, let’s first check if the given fraction can be simplified: factors of 9 are 1, 3, 9; factors of 12 are 1, 2, 3, 4, 6, 12.

The GCF of 9 and 12 is 3. Dividing the numerator and the denominator of the given fraction by the GCF, we get:

\$\frac{9}{12}\$ = \$\frac{9 ÷ 3}{12 ÷ 3}\$ = \$\frac{3}{4}\$

Now let’s convert the simplified fraction \$\frac{3}{4}\$ to percentage.

1. Using division to convert fraction to decimal, we get:

\$\frac{3}{4}\$ = 3 ÷ 4 = 0.75

2. Multiplying by 100 to get percentage, we get:

0.75 × 100 = 75%

Jane’s Chemistry score is 75%.

Answer

Jane’s Chemistry score is \$\frac{9}{12}\$ = \$\frac{3}{4}\$ = 75%, therefore, she has a higher score in Math.

Related Questions

• What is 5/8 as a percent?
• What is 4/5 as a percent?
• What is 1/8 as a percent?
• What is 3/5 as a percent?
• What is 1/6 as a percent?
• What is 1/5 as a percent?