No results found
We can’t find anything with that term at the moment, try searching something else.
Hex Calculator
Online hex calculator performs hex math operations and conversions. Hex addition, hex subtraction, hex multiplication, hex division became fast & easy
| Answer | |
|---|---|
| Decimal to Hex | 170 = AA |
| Hex to Decimal | DAD = 3501 |
| Answer | |
|---|---|
| Hex value | 8AB + B78 = 1423 |
| Decimal value | 2219 + 2936 = 5155 |
There was an error with your calculation.
Table of Contents
- Calculator Application
- Hexadecimal Numbering System
- Decimal to Hexadecimal Conversion
- Hexadecimal to Decimal Conversion
- Hexadecimal Addition
- Hexadecimal Subtraction
- Hexadecimal Multiplication
- The Multiplication in Decimal System
- Hexadecimal Division
- Conclusion

Introducing the Hex Calculator, the ultimate tool for quickly and efficiently performing mathematical operations in hexadecimal notation. This advanced Hexadecimal Calculator can handle a variety of functions related to hexadecimal math, including hexadecimal addition, hexadecimal subtraction, hexadecimal multiplication, and hexadecimal division. It can also act as hexadecimal converter as it can convert numbers written in hexadecimal to decimal and vice versa.
But why is hexadecimal notation important, you may ask? It is widely used in various industries, particularly in computing and technology. Hexadecimal notation provides an efficient way of expressing large binary values in a more manageable form.
The Hex Calculator allows you to easily navigate and analyze hexadecimal values, making problem-solving and analysis more streamlined. You will be able to work with hex math quickly and effortlessly. Hex addition, hex subtraction, hex multiplication, and hex division have never been so easy!
So, take the guesswork out of hexadecimal operations with the Hexadecimal Converter.
Calculator Application
Hexadecimal notation commonly referred to as "hex" for short, is a widely used form of representation in various industries, particularly in computing and technology. These unique numbers, composed of the digits 0-9 and the letters A-F, provide an efficient method of expressing large binary values in a more manageable form.
One of the most prevalent and advantageous applications of hex numbers is found in computer programming. Programmers often utilize hexadecimal values to represent colors, memory addresses, and other data in programming languages such as C, C++, and Java. Additionally, hex conversions are used to perform various mathematical operations and conversions of hexadecimal values within these languages.
Another critical area where hex numbers are employed is digital data storage systems. Professionals in this field use hex numbers for memory addresses and other information stored in hexadecimal format, making navigating and analyzing these systems more streamlined. This can be particularly useful for identifying and resolving problems.
Hex numbers are also employed in networking. Network administrators and engineers use hex numbers to convert decimal and hexadecimal values when working with networking protocols such as IPv4 and IPv6. Understanding the hexadecimal representation of network addresses and other data can be valuable for identifying and resolving issues, optimizing performance, and securing the network.
Digital forensics is another area where hex converters are used extensively. These tools are employed to analyze data and find patterns in hexadecimal format. Hexadecimal format is commonly used to represent binary data, such as images and other multimedia files. Using hex numbers, forensic analysts can view and manipulate a file's raw data, allowing them to uncover hidden information or patterns that may not be visible in the standard file format.
Lastly, hexadecimal numbers are employed in cryptography to convert data into a hexadecimal format. This can make it more difficult for unauthorized parties to read or understand the transmitted information. Hexadecimal notation offers a higher level of security as it can conceal data in a format that is not easily recognizable by those without the necessary knowledge and tools to convert it back to its original form. Additionally, the hexadecimal notation can also be used in the creation of cryptographic keys, which are essential for secure communication and data transfer.
Overall, hexadecimal numbers are a powerful tool that can be utilized in many applications, from computer programming and digital data storage to networking, digital forensics, and cryptography. Their compact and easy-to-read nature makes them valuable tools for professionals in many fields.
Hexadecimal Numbering System
The hexadecimal system is a way of representing numbers with a base of 16. This means that instead of 10 digits like the decimal system or 2 digits like the binary system, the hexadecimal system uses 16 digits, including 0-9, and the letters A, B, C, D, E, and F. These letters represent numbers 10-15.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
The hexadecimal system has some unique advantages compared to the decimal and binary systems. For example, each hexadecimal digit represents 4 binary digits, called nibbles. This system simplifies the representation of large binary numbers.
For example, the binary value 1010101010 can be represented as 2AA in hexadecimal format. This helps computers compress large binary values so that they can be easily converted between the two systems.
Hexadecimal values are often used in computer science and programming because they are easier to read and understand than binary values. Using letters and numbers makes it easier to identify specific values and patterns in the code.
Decimal to Hexadecimal Conversion
This process may seem complicated at first, but it becomes relatively simple with some practice and understanding of the meaning of places in different number systems. You can use our hexadecimal converter to make the process quicker. But if you understand the principles of converting hexadecimal numbers, it will be easier for you to work with them in the future.
Converting a decimal number to its hexadecimal equivalent involves repeatedly dividing a decimal number by 16 and writing down the remainder each time.
Let's convert the decimal number 568 to hexadecimal.
- Divide this decimal number by 16 and write down the value of the remainder and the quotient.
568 / 16 = 35.5
568 = (35 × 16) + 8
The remainder of the division is 8. The quotient is 35.
- Convert the remainder of the decimal digit to a hexadecimal digit.
8₁₀ = 8₁₆
- Repeat the first and second steps with the quotient from the previous step.
35 / 16 = 2.1875
35 = (2 × 16) + 3
The remainder of the division is 3. The quotient is 2.
3₁₀ = 3₁₆
2 / 16 = 0.125
2 = (0 × 16) + 2
The remainder of the division is 2. The quotient is 0.
2₁₀ = 2₁₆
- After performing the previous steps, we have three remainders.
The first remainder is the last (rightmost) digit of the hexadecimal number, and the last remainder is the first digit of our hexadecimal number. From these remainders, you can get a hexadecimal number:
568₁₀ = 238₁₆
Note that when the remainder is greater than 9, the corresponding hexadecimal digit is represented by the letters A-F.
Converting a decimal number to hexadecimal means dividing the decimal number by 16, accounting for the remainder, and repeating the process until the quotient is 0. The reminders obtained in the process are used to form the hexadecimal representation of the decimal number.
Hexadecimal to Decimal Conversion
Converting a hexadecimal number to its decimal equivalent involves multiplying each digit of the hexadecimal number by the corresponding place value and adding up the results. Below is a step-by-step explanation with an example:
Convert 1B7E hexadecimal number to a decimal number.
- Designate the index of each digit in a hexadecimal number. The index is simply the digit's position in the number, counting from right to left.
| HEX | 1 | B | 7 | E |
|---|---|---|---|---|
| Index | 3 | 2 | 1 | 0 |
- Replace the digits with equivalent decimal values according to the given mapping:
| HEX | 1 | 11 | 7 | 14 |
|---|---|---|---|---|
| Index | 3 | 2 | 1 | 0 |
- Now multiply each digit of the hexadecimal number by 16, raised to the power of the corresponding index.
| HEX | 1×163=4096 | 11×162=2816 | 7×161=112 | 14×160=14 |
|---|---|---|---|---|
| Index | 3 | 2 | 1 | 0 |
- Add all the values to get the decimal equivalent.
1B7E = 4096 + 2816 + 112 + 14 = 7038
To summarize, converting a hexadecimal number to a decimal consists of multiplying each digit by its corresponding place value and adding the results. The sum of these calculations is the final decimal representation.
Hexadecimal Addition
Long Addition
When working with numbers in the hexadecimal system, adding them is quite similar to how we add numbers in the decimal system. We begin by aligning the digits on the right side and adding the corresponding digits together.
However, it's essential to remember that the highest value a single hexadecimal digit can represent is 15. So, if the sum exceeds 15, we must carry over the one to the next column, just as we would in decimal addition.
It's crucial to follow the correct order of operations, starting with the rightmost digits and moving towards the left as we work our way through the digits. And, just like in decimal addition, we must carry over the one if the sum exceeds 15.
Example
Let's add the following numbers using the long addition method:
AB2136 + 1C89A5
We add up from the smallest digits. Move from right to left, adding the corresponding digits (6+5, 3+A, 1+9, 2+8, B+C, A+1).
6₁₆+ 5₁₆ = 6₁₀ + 5₁₀ = 11₁₀ = B₁₆
3₁₆ + A₁₆ = 3₁₀ + 10₁₀ = 13₁₀ = D₁₆
1₁₆ + 9₁₆ = 1₁₀ + 9₁₀ = 10₁₀ = A₁₆
2₁₆ + 8₁₆ = 2₁₀ + 8₁₀ = 10₁₀ = A₁₆
B₁₆ + C₁₆ = 11₁₀ + 12₁₀ = 23₁₀ here, the sum is more than 15, so we subtract 16, that is 23₁₀ - 16₁₀ = 7₁₀ and the one goes to the next digit
A₁₆ + 1₁₆ = 10₁₀ + 1₁₀ = 11₁₀ and we add one from the previous digit to the obtained sum, i.e. 11₁₀ + 1₁₀ = 12₁₀ = С₁₆
So, we ended up with the following:
AB2136 + 1C89A5 = C7AADB
Hexadecimal Subtraction
Long Subtraction
The process of subtraction in the hexadecimal system is quite similar. First, we start with the rightmost digits and work our way to the left. If the number we're subtracting is larger than the one we're subtracting from, we borrow from the next digit to the left. To borrow, we must add 16 (10 in decimal) to the number we're subtracting from and subtract 1 from the next digit.
Keeping track of the borrowed values as we move along the digits is important. The process may seem familiar, but it's crucial to remember that we are working within the hexadecimal system, where the highest value a single digit can represent is 15.
Overall, hex subtraction is a simple task, but it requires a bit of attention to detail to ensure we use the correct values and keep track of borrowed values.
Example
Let's find the difference between the following numbers using long subtraction:
AB2136
1C89A5
Subtract beginning with the smallest digits. Move from right to left, subtracting the corresponding digits (6-5, 3-A, 1-9, 2-8, B-C, A-1).
6₁₆ - 5₁₆ = 6₁₀ - 5₁₀ = 1₁₀ = 1₁₆
3₁₆ - A₁₆ = 3₁₀ - 10₁₀ we get a difference less than zero, so we take one from the next digit, that is (3₁₀ + 16₁₀) - 10₁₀ = 9₁₀ = 9₁₆
1₁₆ - 9₁₆ now, because of the previous borrowing, we have not 1₁₆ but 0₁₆, so we retake one from the next digit, that is (0₁₀ + 16₁₀) – 9₁₀ = 7 10 = 7₁₆
2₁₆ - 8₁₆ now, because of the previous borrowing, we have not 2₁₆ but 1₁₆, so we take again one from the next digit, that is (1₁₀ + 16₁₀) - 8₁₀ = 910 = 9₁₆
B₁₆ - C₁₆ = 11₁₀ - 12₁₀ now, because of the previous borrowing, we don't have 11₁₀ but 10₁₀, so we retake one from the next digit, so (10₁₀ + 16₁₀) - 12₁₀ = 14₁₀ = E₁₆
A₁₆ - 1₁₆ = 10₁₀ - 1₁₀ now because of the previous borrowing we don't have 10₁₀ but 9₁₀, so we calculate 9₁₀ - 1₁₀ = 8₁₀ = 8₁₆
We end up with the following:
AB2136 + 1C89A5 = 8E9791
Hexadecimal Multiplication
Long Multiplication
In hex multiplication, we can use the same basic rules as in decimal multiplication. Line the numbers on top of each other, and start by multiplying the rightmost digits.
Each digit in one number is multiplied by each digit in the other number. In the end, the products are added together.
There is a difference with decimal multiplication. Instead of carrying over a one when the product is greater than 9, a one is carried over when the product is greater than 15.
The result of the multiplication is then represented in hexadecimal format.
When multiplying hexadecimal numbers, you need to convert each number to decimal, perform the multiplication and convert the result back to hexadecimal.
Hexadecimal multiplication can be simplified using a hexadecimal multiplication table.
Hexadecimal Multiplication Table
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
| 2 | 2 | 4 | 6 | 8 | A | C | E | 10 | 12 | 14 | 16 | 18 | 1A | 1C | 1E | 20 |
| 3 | 3 | 6 | 9 | C | F | 12 | 15 | 18 | 1B | 1E | 21 | 24 | 27 | 2A | 2D | 30 |
| 4 | 4 | 8 | C | 10 | 14 | 18 | 1C | 20 | 24 | 28 | 2C | 30 | 34 | 38 | 3C | 40 |
| 5 | 5 | A | F | 14 | 19 | 1E | 23 | 28 | 2D | 32 | 37 | 3C | 41 | 46 | 4B | 50 |
| 6 | 6 | C | 12 | 18 | 1E | 24 | 2A | 30 | 36 | 3C | 42 | 48 | 4E | 54 | 5A | 60 |
| 7 | 7 | E | 15 | 1C | 23 | 2A | 31 | 38 | 3F | 46 | 4D | 54 | 5B | 62 | 69 | 70 |
| 8 | 8 | 10 | 18 | 20 | 28 | 30 | 38 | 40 | 48 | 50 | 58 | 60 | 68 | 70 | 78 | 80 |
| 9 | 9 | 12 | 1B | 24 | 2D | 36 | 3F | 48 | 51 | 5A | 63 | 6C | 75 | 7E | 87 | 90 |
| A | A | 14 | 1E | 28 | 32 | 3C | 46 | 50 | 5A | 64 | 6E | 78 | 82 | 8C | 96 | A0 |
| B | B | 16 | 21 | 2C | 37 | 42 | 4D | 58 | 63 | 6E | 79 | 84 | 8F | 9A | A5 | B0 |
| C | C | 18 | 24 | 30 | 3C | 48 | 54 | 60 | 6C | 78 | 84 | 90 | 9C | A8 | B4 | C0 |
| D | D | 1A | 27 | 34 | 41 | 4E | 5B | 68 | 75 | 82 | 8F | 9C | A9 | B6 | C3 | D0 |
| E | E | 1C | 2A | 38 | 46 | 54 | 62 | 70 | 7E | 8C | 9A | A8 | B6 | C4 | D2 | E0 |
| F | F | 1E | 2D | 3C | 4B | 5A | 69 | 78 | 87 | 96 | A5 | B4 | C3 | D2 | E1 | F0 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | A0 | B0 | C0 | D0 | E0 | F0 | 100 |
If the table is unavailable, each step requires a manual conversion between decimal and hexadecimal.
Example
Let's try multiplying the numbers AB × 1F using long multiplication.
As in traditional long multiplication, we multiply F × B, F × A. Then we multiply 1 × A, 1 × B, and sum up the results, considering the digits of the obtained numbers.
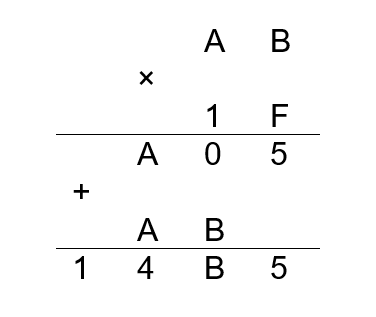
- F × B = A5 – we move A to the next digit, leaving 5
- F × A = 96 – we add to it A from the previous digit and get A0
- 1 × B = B
- 1 × A = A
Add up the intermediate results (A05 + AB0) and we get AB × 1F = 14B5
The Multiplication in Decimal System
The second approach to multiplication is to perform multiplication operations on decimal numbers directly. You can convert hex numbers to decimal numbers, multiply them in decimal format and then convert them back to hexadecimal.
In this example, "AB" in decimal is 171, and "1F" in decimal is 31.
Perform the multiplication in decimal format. In this example, 171 × 31 = 5261.
Convert the result from decimal 5261₁₀ to hexadecimal to get 14B5₁₆.
AB₁₆ × 1F₁₆ = 171₁₀ × 31₁₀ = 5261₁₀ = 14B5₁₆
The result is: AB₁₆ × 1F₁₆ = 14B5₁₆
Hexadecimal Division
Long Division
Hex division is similar to decimal division. It also involves dividing a dividend by a divisor to find the quotient. However, instead of using 10 as the base, hex division uses 16.
Divide the dividend by the divisor as you would with decimal division, using the same basic steps of repeated subtraction and bringing down the next digit of the dividend.
Keep track of the remainder, the amount left over after each subtraction. Once the division is complete, you will have the quotient in hexadecimal form, which is the final result.
Example
Let's divide 9CC0C by A using a long division.
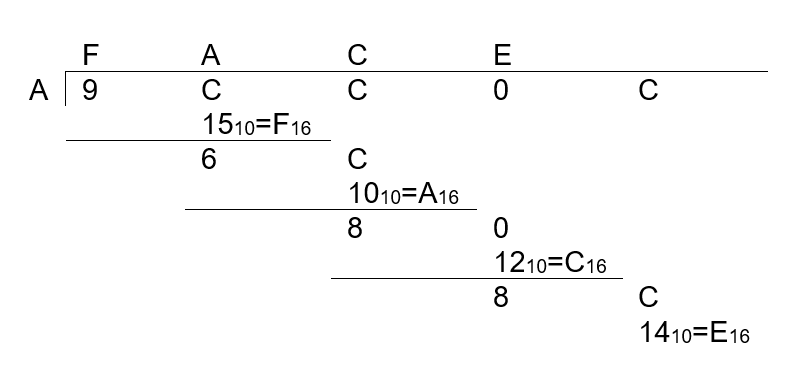
Let's try to divide 9CC0C by A
- 9C₁₆ / A₁₆ = 156₁₀ / 10₁₀ = 15₁₀ + remainder 6 = F₁₆ + remainder 6 We use F as the first digit of our quotient. 6 can't be divided by A, so we take the digit C from the next position. Now we divide 6C / A
- 6C₁₆ / A₁₆ = 108₁₀ / 10₁₀ = 10₁₀ + remainder 8 = A₁₆ + remainder 8 We use A as the second digit of our quotient. 8 can't be divided by A, so we take the digit 0 from the next position. Now we divide 80 / A
- 80₁₆ / A₁₆ = 128₁₀ / 10₁₀ = 12₁₀ + remainder 8 = C₁₆ + remainder 8 We use C as the third digit of our quotient. 8 can't be divided by A, so we take the digit C from the next position. Now we divide 8C / A
- 8C₁₆ / A₁₆ = 140₁₀ / 10₁₀ = 14₁₀ = E₁₆
We end up with 9CC0C / A = FACE due to division.
The Division in Decimal System
According to the second method, you can convert the hex numbers to decimal, perform the division in decimal format, and then convert the result back to hexadecimal f.
In this example, "9CC0C" in decimal is 642060 and "A" in decimal is 10.
Perform the division in decimal format. In this example, 642060 / 10 = 64206.
Convert the result from decimal 64206₁₀ to hexadecimal to get FACE₁₆.
9CC0C₁₆ / A₁₆ = 642060₁₀ / 10₁₀ = 64206₁₀ = FACE₁₆
The result is: 9CC0C₁₆ / A₁₆ = FACE₁₆
As with hexadecimal multiplication, having a hexadecimal multiplication table can be useful when performing hexadecimal division.
Conclusion
If you need a tool to take your hex numbers to the next level, check out Hex Calculator.
This powerful tool is like a secret weapon for anyone working in computing and technology, as well as many other fields that rely on hexadecimal notation. It's a versatile companion that can easily perform various mathematical operations and conversions, leaving you free to focus on the bigger picture.
With the Hex Calculator, you can add, subtract, multiply, and divide hexadecimal numbers with the precision of a pro and convert numbers written in hexadecimal to decimal and vice versa with a few simple clicks.
Its ease of use and accuracy make it an ideal tool for streamlining and simplifying complex calculations.