No results found
We can’t find anything with that term at the moment, try searching something else.
Area Calculator
Area calculator to find the surface area of the following shapes - rectangle, triangle, circle, sector, ellipse, trapezoid, and parallelogram.
| Result | |
|---|---|
| Square Meters | 80 m² |
| Square Footage | 861.112833 ft² |
| Square Inches | 124000.248 in² |
| Square Yards | 95.6792037 yd² |
| Acres | 0.019768413 ac |
| Hectares | 0.008 ha |
There was an error with your calculation.
Table of Contents

This calculator allows you to find the surface area of the most common shapes – rectangle, triangle, trapezoid, circle, sector, ellipse, and parallelogram. Since area describes the size of a surface, this calculator can be used as a land area calculator.
Directions for use
To use this area finder, choose the figure for which the area has to be calculated, and enter the known values in their respective fields. Choose units for each value from the drop-down menus. Then press "Calculate." The calculator will find the figure's area, demonstrate the area value, and the solution algorithm.
Note that if the given values were input in several different units, the solution would be expressed in each. You can also click on the "Show results in other units" at the end of the solution to convert the result to the necessary units.
Limitations on the input values
For all calculators, input values should be represented by positive integers or decimals. 0 is also a possible input.
Some calculators have additional limitations, which are listed below.
Triangle
The sum of any two edges must be larger than the third edge.
Sector
The angle value should be between 0 and 360 degrees or between 0 and 6.2831853071796 radians.
Note that you cannot use "pi" to enter angle values in radians. You will need to calculate the radian angle value first. For example, if you have a 45° angle that you want to enter in radians, you will need to perform the following calculation: 45° = π/2 = 0.785398 rad. Then you enter 0.785398 as the angle value.
Formulas and calculation examples
The area describes the size of a surface. Area value demonstrates how many unit squares can fit within a given two-dimensional figure. One square meter is the standard size of the unit square, as defined by the International System of Units (SI). One square meter, or 1 m², describes the area of a square with a 1m side length:
Rectangle
The area of a rectangle describes the number of unit squares that can fit within the rectangle's borders. For example, the area of a rectangle with side lengths of 3 meters and 2 meters can be calculated by dividing the surface into unit squares and counting the number of those squares:
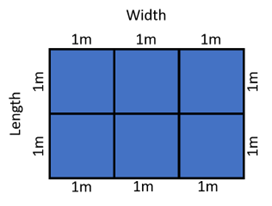
Area = 6 m²
The formula for calculating the rectangle area can be written as:
Area = Width × Length
or
A = w × l
Where A is the area, w is the width, and l – is the length of the rectangle.
Calculation example
Imagine you are doing some renovations in your house, and you decide to put new tiles on the bathroom floor. You know that the bathroom has a rectangular shape with a length of 1.5 meters and a width of 2 meters. What is the surface area you will need to cover with the tiles?
Solution
- Width = w = 2m
- Length = l = 1.5m
Use the rectangle area formula to find the surface area of the bathroom floor:
A = w × l = 1.5 × 2 = 3 m²
You will need to cover an area of three square meters.
Triangle
There are several formulas for calculating the triangle area. This area calculator uses the semi-perimeter formula or Heron's formula:
$$A=\sqrt{s(s-a)(s-b)(s-c)}$$
Where A is the area of the triangle, a, b, and c – are the side lengths, and s – is the semi-perimeter of the triangle, calculated as follows:
s = (a + b + c)/2
Calculation example
John inherited a triangular piece of land. He knows that the side lengths of his land are 45 meters, 27 meters, and 31 meters. How much land does John own now?
Solution
- Side 1 = a = 45m
- Side 2 = b = 27m
- Side 3 = c = 31m
Let’s calculate the semi-perimeter:
s = (a + b + c)/2 = (45 + 27 + 31)/2 = 103/2 = 51.5
Then let’s use Heron’s formula to calculate the area:
$$A=\sqrt{s(s-a)(s-b)(s-c)} = \sqrt{51.5(51.5-45)(51.5-27)(51.5-31)} = \sqrt{51.5×6.5×24.5×20.5} = \sqrt{168128.1875} = 410$$
John owns 410 m² of land.
Trapezoid
The area of a trapezoid can be calculated with the help of the following formula:
A = 1/2 × (b₁ + b₂) × h
where b₁ and b₂ are the bases of the trapezoid (the parallel sides of the trapezoid), and h – is its height.
Calculation example
Mary has an old trapezoid table, which she wants to refinish. The furniture restoration shop charges $150 per square meter of the surface. If the dimensions of her table are b₁ = 2m, b₂ = 1.5m, and h = 1m, how much will Mary have to pay to refinish her table?
Solution
- b₁ = 2m
- b₂ = 1.5m
- h = 1m
Let's first calculate the surface area of the table using the trapezoid area formula:
A = 1/2 × (b₁ + b₂) × h = 1/2 × (2 + 1.5) × 1 = 1/2 × 3.5 × 1 = 1.75
The surface of Mary's table is 1.75 m². To calculate the total price, we need to multiply the surface area by the price per square meter:
Total price = A × price per m² = 1.75 × 150 = 262.5
Mary will have to pay $262.5 to refinish her table.
Circle
The area of a circle is calculated with the help of the following formula:
A = π × r²
where π ≈ 3.1415926, and r is the radius of the circle.
Calculation example
A lawn sprinkler has a radius of up to 5 meters. Will one lawn sprinkler be enough to water a circular lawn of 60m²?
Solution
The lawn sprinkler rotates and covers a distance of 5m in every direction.
r = 5m
Let’s calculate the maximum lawn area covered by the sprinkler:
A = π × r² = 3.1415926 × 5² = 3.1415926 × 25 ≈ 78.5
The lawn sprinkler covers an area of 78.5 m². Therefore, one sprinkler will be enough for a 60 m² lawn.
Sector
If a sector is expressed through the angle in degrees, the surface area of the sector can be calculated with the following formula:
A = (angle/360) × π × r²
Where angle – is the defining angle of the sector, r is the radius, and π ≈ 3.1415926.
If the sector is defined through an angle in radians, the surface area can be calculated as follows:
A = (angle/2) × r²
where angle – is the defining angle of the sector, and r is the radius.
Ellipse
The surface area of an ellipse can be calculated with the help of the following formula:
A = π × a × b
where π ≈ 3.1415926, a is half of the larger axis of the sector, and b is half of the smaller axis of the ellipse.
Parallelogram
The surface area of a parallelogram can be calculated as follows:
A = b × h
where b is the base of the parallelogram, and h – is its height.