No results found
We can’t find anything with that term at the moment, try searching something else.
Triangle Calculator
The triangle calculator finds all triangle measurements – side lengths, triangle angles, area, perimeter, semiperimeter, heights, medians, inradius, and circumradius.
| EQUILATERAL ACUTE TRIANGLE | |||
|---|---|---|---|
| Side a | 5 | Angle A | 60° = 1.047198 rad |
| Side b | 5 | Angle B | 60° = 1.047198 rad |
| Side c | 5 | Angle C | 60° = 1.047198 rad |
| Area | 10.82532 | Height ha | 4.330127 |
| Perimeter p | 15 | Height hb | 4.330127 |
| Semiperimeter s | 7.5 | Height hc | 4.330127 |
| Median ma | 4.330127 | Inradius r | 1.443376 |
| Median mb | 4.330127 | Circumradius R | 2.886751 |
| Median mc | 4.330127 | ||
There was an error with your calculation.
Table of Contents
- Triangle calculator
- Directions for use
- Limitations on the input values
- Calculation example
- Triangle: definition and important formulas
- Conditions of existence of a triangle
- Triangle measurements

Triangle calculator
The triangle calculator is an online triangle solver allowing you to find all triangle measurements based on three known measurements quickly. The calculator takes the lengths of the sides of a triangle and triangle angles as inputs and calculates the following measurements:
- missing side lengths,
- missing triangle angles,
- area,
- perimeter,
- semiperimeter,
- heights to all sides of the triangle,
- medians to all sides of the triangle,
- inradius,
- circumradius.
The calculator also provides the coordinates of the vertices, the centroid, the inscribed circle center, and the circumscribed circle center, assuming that the coordinates of vertex A are [0, 0].
Directions for use
To use this triangle calculator, enter any three values into the input fields. You can enter the values of any angles or any side lengths. Note that at least one of the values has to represent a side length; otherwise, a triangle will have infinite solutions.
After entering the values, select the units for triangle angles. You can choose between degrees or radians. When selecting radians, use "pi" to represent π. For example, if the angle value is \$\frac{π}{3}\$, enter "pi/3." After inserting the known values, press "Calculate." The calculator will return all missing values from the list above and the schematic view of the triangle, which will help you better visualize it.
After the answer, you can expand the following field - Show Calculation Steps – to get familiar with the solution algorithm and the formulas used to find the answer.
Limitations on the input values
At least one of the known values must be a side length.
When entering the following combination of values – two angles and one side length – note that the sum of the angle values has to be less than 180° or π.
When entering three side lengths, note that the sum of any two side lengths should be greater than the length of the remaining side.
Calculation example
Imagine you are moving and want to borrow a truck from a friend. You will need to load and unload the truck, but it doesn't have a built-in ramp. You have a portable ramp, but you must ensure its dimensions fit the truck's height. Your ramp is not adjustable, and you have measured that its two sides measure as 1 m and 0.8 m, and the angle opposite to the side of 1 m is 85 degrees (see the image). You know that you can adjust the truck's height from 0.5 m to 1 m. Does your ramp fit?
Given
- side b = 1;
- side c = 0.8;
- angle B = 85 degrees.
Solution
To determine whether your ramp fits the truck, you need to solve the triangle above and estimate whether the length of side A fits the given range for the truck's height: 0.5< a < 1.
Inserting the values presented above into the triangle calculator, you get the following answer in the task, we will only need the missing side length.
So the rest of the answers are not demonstrated in this practical example, while the triangle solver still calculates them:
Answer
-
Side a = 0.67376
-
Side b = 1
-
Side c = 0.8
-
angle A = 42.16° = 42°9'35" = 0.73582 rad
-
angle B = 85° = 1.48353 rad
-
angle C = 52.84° = 52°50'25" = 0.92224 rad
The ramp looks something like this:
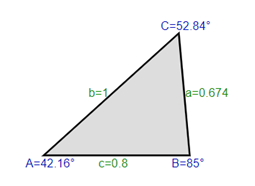
We see that a ≈ 0.674, and we know that the height of the truck can be adjusted in the range 0.5 < a < 1. This means that the ramp height fits the adjustable height of the truck, and you can borrow the truck from your friend instead of renting one!
Triangle: definition and important formulas
In geometry, a triangle is a plane figure made by the intersection of three straight non-parallel lines. A triangle can also be described as a polygon with three vertices and three edges. The edges of the triangle are usually called sides.
Conditions of existence of a triangle
Two conditions define the existence of a triangle; one condition is applied on the sides, and the other – on the angles. The condition on the sides is based on the triangle inequality. It states that the sum of the lengths of any two sides of the triangle must be greater than or equal to the length of the remaining third side. If the sum of the lengths of the two sides equals the length of the third side, the triangle is called degenerate.
A degenerate triangle is a triangle where all three vertices lie on the same straight line. It's a very special triangle case, usually not discussed in elementary geometry, and is, therefore, not considered here.
The condition on the angles states that the sum of the three angles of any triangle always equals 180° or π radians.
Triangle measurements
Let's define the most crucial triangle measurements and look at the formulas for calculating their values.
The perimeter of a triangle is the sum of the lengths of all its sides and can be found as follows:
p = a + b + c
The semiperimeter of a triangle – is half of the length of the perimeter of the triangle:
$$s=\frac{p}{2}=\frac{a+b+c}{2}$$
The area of a triangle – is a property describing how much space the triangle takes up on a plane. If the lengths of the two sides of the triangle and the angle between these two sides are known, the area of a triangle can be calculated as follows:
$$A=\frac{1}{2}a× b×\sin{C}$$
A triangle's height, or altitude, is perpendicular from one of the angles to the opposite side. Since any triangle has three sides, any triangle will also have three perpendiculars. A height perpendicular to side A is usually denoted as hₐ. Similarly, the other two heights are denoted as \$h_b\$ and h꜀. The easiest way to find the height of a triangle is through its area:
$$A=\frac{1}{2}× a× h_a=\frac{1}{2}× b× h_b=\frac{1}{2}× c× h_c$$
$$h_a=\frac{2A}{a}, h_b=\frac{2A}{b}, h_c=\frac{2A}{c}$$
Median to a side of a triangle – is the line from a vertex of the triangle to the middle of the opposite side. Any triangle has three medians.
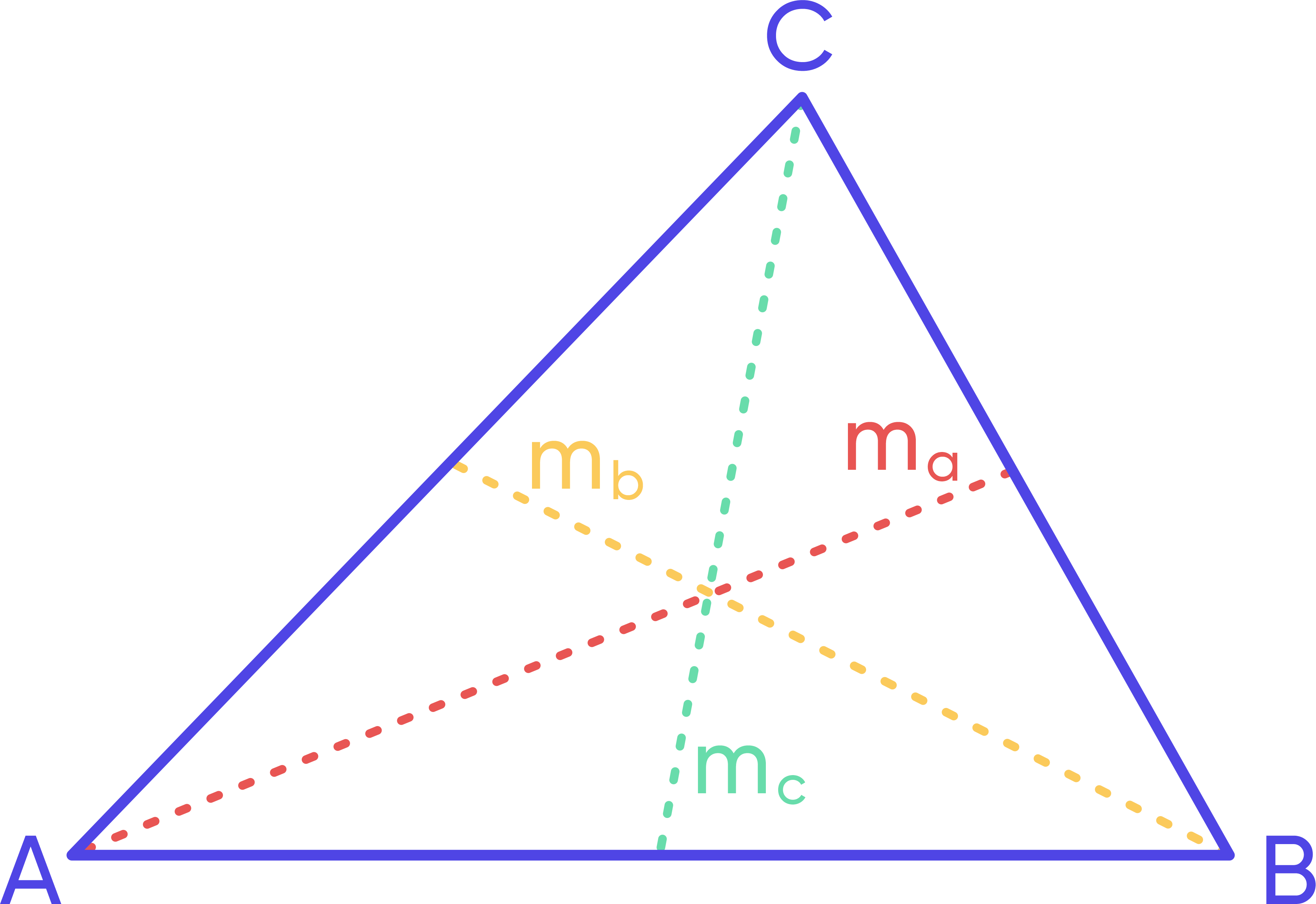
A median to side a is usually denoted as mₐ. Similarly, the other two medians are denoted as \$m_b\$ and m꜀. We can find the lengths of the medians with the following formula:
$$m_a=\frac{1}{2}\sqrt{2b²+2c^2-a^2}$$
The inradius of a triangle – is the radius of a circle inscribed inside the triangle and touching all of its sides.
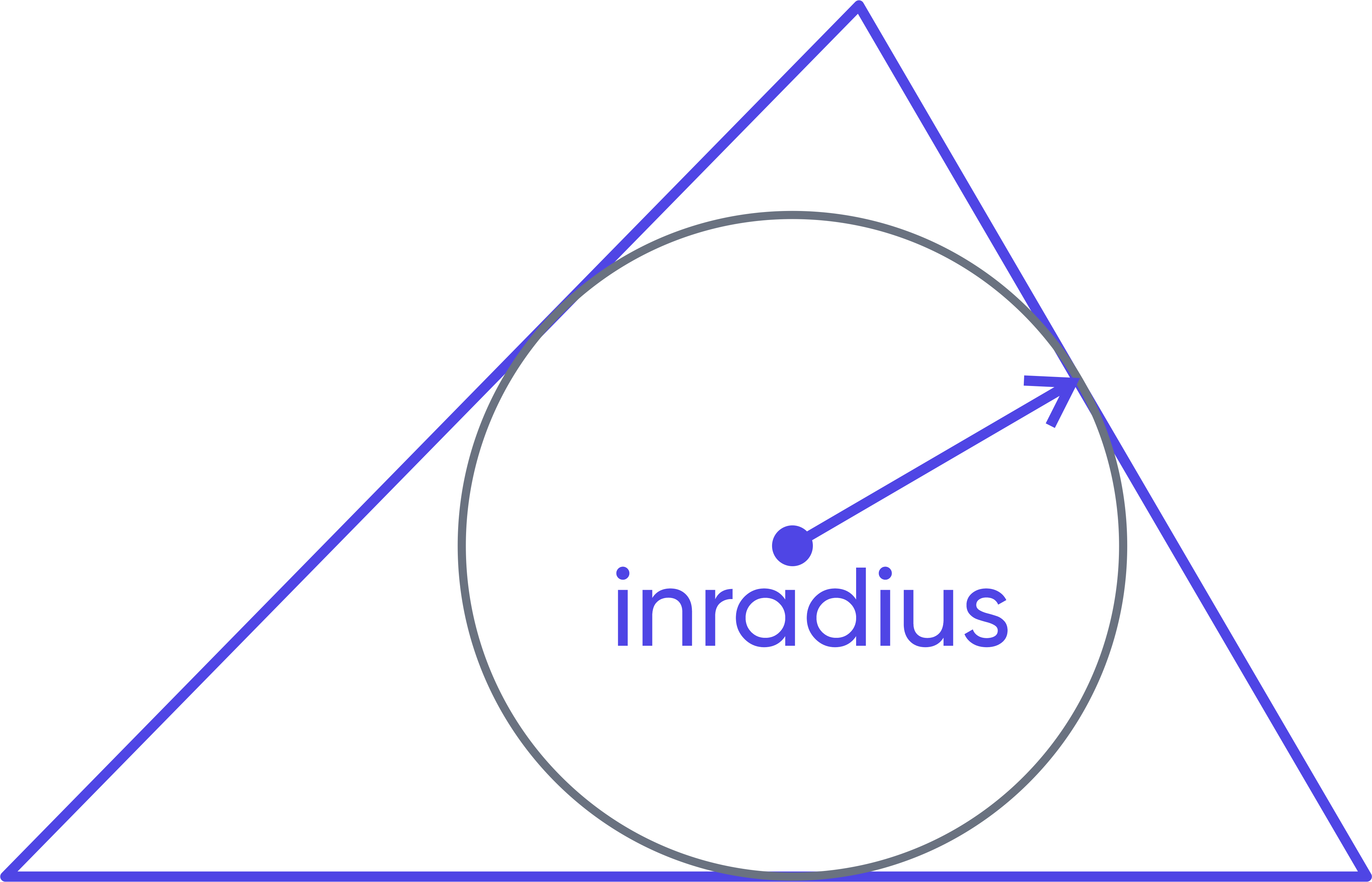
The length of the inradius r can be found as follows:
$$r=\frac{A}{s}$$
The circumradius of a triangle – is the radius of a circle passing through all three vertices of the triangle.

We can find the length of the circumradius R from the sine rule:
$$2R=\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}$$
The sine rule is also beneficial for finding the missing values of side lengths or angles of a triangle. Another helpful rule is the cosine rule:
$$a=\sqrt{b²+c^2-2bc\cos{A}}$$
$$b=\sqrt{a^2+c^2-2ac\cos{B}}$$
$$c=\sqrt{a^2+b²-2ab\cos{C}}$$
The formulas listed above allow calculating all triangle measurements. The triangle calculator uses these formulas to find the missing values.