Proportion Calculator

Ratio calculator finds a missing ratio value from the input proportion. In other words, it converts a ratio to an equivalent ratio based on one known value of the new ratio.

Directions for use

Ratio calculator

Use the calculator when given a proportion with one missing value. The calculator finds a missing value from the following proportion:

A : B = C : D

To use the calculator, enter any three of the values – A, B, C, and D, and press “Calculate.” The calculator will return the missing value and several visual representations of the ratio, including a pie chart, a bar chart, and a rectangle with side lengths corresponding to the numbers of the given ratio. The visual representations will correspond to the ratio, both numbers of which were initially known.

For example, if you enter the values of A, B, and C, the ratio finder will return the value of D and the visual representations of the A : B ratio. If you enter the values of B, C, and D, the ratios calculator will return the value of A, and the visual representations of the C : D ratio.

Ratios and Proportions

Ratio definition

A ratio is a mathematical way of comparing two values. A ratio represents how many times one value can contain another value. Ratios are usually written as two numbers separated by a colon symbol. For example, 1 : 3, or 5 : 9. They can also be expressed using the word “to”, or written as fractions. Below are some possible ways to write down ratios:

9:4

1 to 3

4/5 or \$\frac{4}{5}\$

Ratios can be visually represented as pie charts or bars. For example, the ratio of 1 to 3 can be alternatively written down as 1 : 3, or 1/3, and represented as follows:

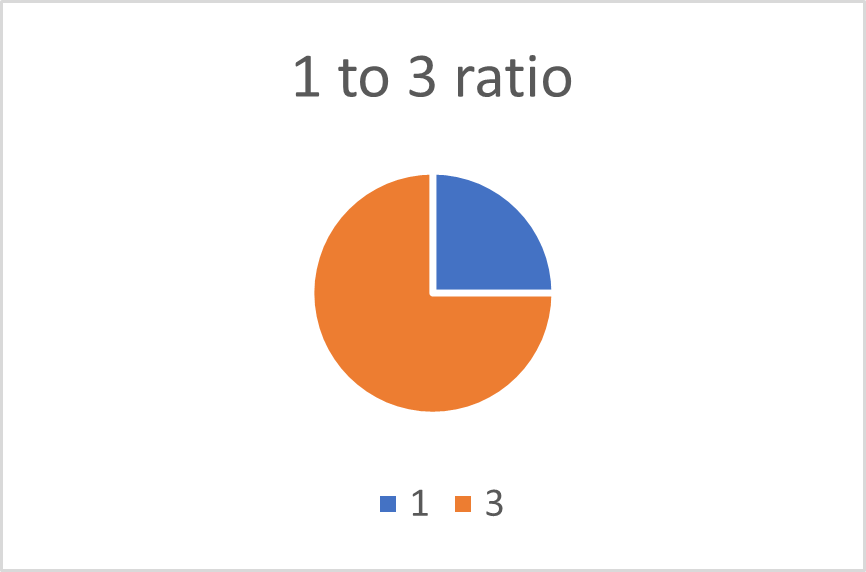
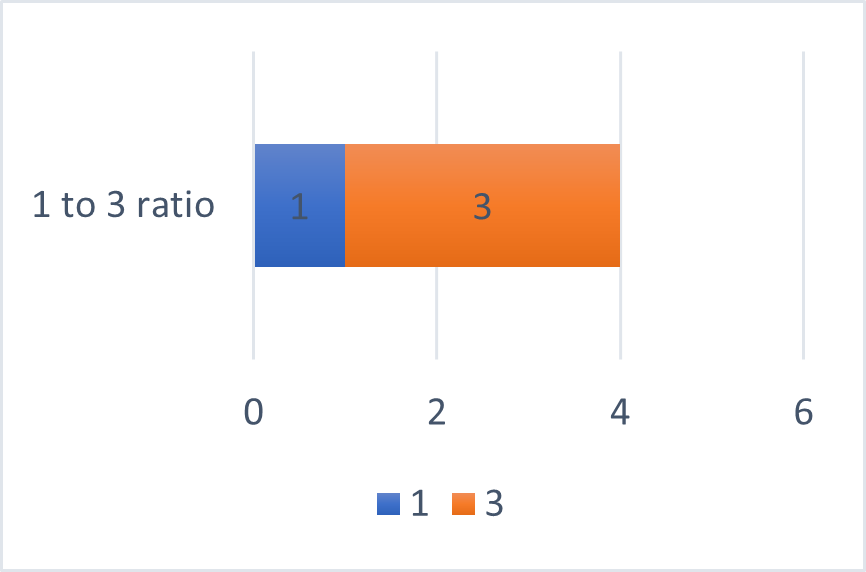
Scaling ratios

Ratios can be scaled up or down. To scale a ratio up, multiply both numbers of the ratio by a given number. For example, to enlarge the 1 : 3 ratio 4 times, multiply both 1 and 3 by 4:

1 : 3 = (1 × 4) : (3 × 4) = 4 : 12

Note that the final ratio is equivalent to the initial ratio since the final fraction 4/12 can be simplified to the initial fraction 1/3. To scale a ratio down, divide both numbers of the ratio by a given number. For example, to shrink the 25 : 70 ratio 5 times, divide both 25 and 70 by 5:

25 : 70 = (25/5) : (70/5) = 5 : 14

Also, the final ratio is equivalent to the initial ratio since the initial fraction 25/70 can be simplified to the final fraction 5/14.

Example 1

Scaling ratios is very often used while cooking when you need to scale a recipe to accommodate a different number of people. For example, a pancake recipe feeding one person requires half a cup of flour and one cup of milk. You need to make pancakes for a family of 8. How would you scale the amount of ingredients?

Solution

The initial ratio can be written as follows:

0.5 : 1

You need to make pancakes for a family of 8, so you must scale up the given ratio 8 times. To do that, you have to multiply both numbers of the initial ratio by 8:

0.5 : 1 = (0.5 × 8) : (1 × 8) = 4 : 8

The final ratio is 4 : 8

Proportions

A proportion is an equation of two ratios. For example,

1 : 2 = 2 : 4

5 : 6 = 30 : 36

Proportions have a property that is very useful for calculating ratios – the cross-product property. This property states that the product of the means (the inner numbers of the proportion) is equal to the product of the extremes (the outer numbers of the proportion).

For example, in the above proportion 5 : 6 = 30 : 36, 6 and 30 – are the means, and 5 and 36 are the extremes. According to the cross-product property of proportions, 6 × 30 = 5 × 36. Check this: 6 × 30 = 180, and 5 × 36 = 180.

Example 2

Ratios or aspect ratios are often used to describe screen sizes and video dimensions.

For example, cameras' most common 480p resolution is usually characterized by the 4 : 3 aspect ratio. The height of the video is smaller than the width and is equal to 480 pixels. What is the width of the video in pixels?

Solution

We know that the aspect ratio is 4 : 3. This will be one of the ratios of the proportion. We also know that the height of the video is smaller than the width. Therefore, the height value will be the second value in the second proportion. Based on the given data, we can write the following proportion:

4 : 3 = Width : Height

4 : 3 = Width : 480

We can find the width using the cross-product property of proportions:

3 × Width = 4 × 480

Width = (4 × 480)/3 = 1920/3 = 640

A video of 480p resolution, characterized by the 4 : 3 aspect ratio, will have a width of 640 pixels and a height of 480 pixels.

Note that some devices use different aspect ratios to define the resolution. That results in the different widths of the video files. For example, iPod Touch 4 uses 480p (3:2) resolution, with 720 × 480 width and height, respectively. Samsung Galaxy S II uses 480p (5:3) resolution, with 800 × 480 pixels for video width and height, respectively.