Pythagorean Theorem Calculator

This Pythagorean calculator finds the length of a side of a right triangle if the other two sides of the triangle are known. The calculations are performed based on the Pythagorean theorem.

Directions for use

Enter the known side lengths and press "Calculate." The calculator will return the following values:

• Length of the third side.
• Angle values of the non-90° angles in degrees and radians.
• Area of the triangle.
• Perimeter of the triangle.
• Length of the altitude perpendicular to the hypotenuse.

The calculator will also return the detailed solution, which you can expand by pressing "+ Show Calculation Steps."

Note that the input fields for each side include a whole number part and a square root part so that you can conveniently enter values like 2√3, √3, etc.

Note also that the values of a and b, the legs of the triangle, have to be shorter than the value of c, the hypotenuse.

Pythagorean Theorem

Pythagoras' theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the cathetuses.

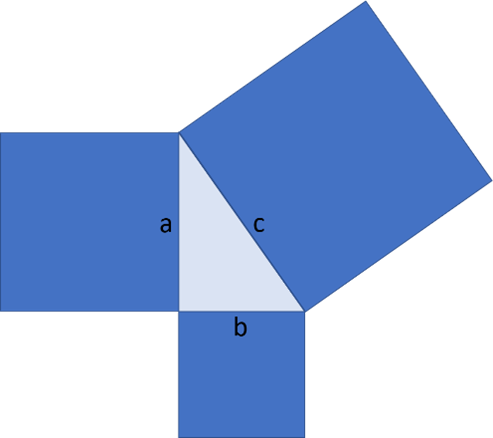
The pythagorean theorem can be written as follows:

a² + b² = c²,

Where a and b are the lengths of the shorter sides, or legs, of a right triangle, and c – is the length of the longest side or hypotenuse. The equation above can be described as follows: a squared plus b squared equals c squared.

Proof of the Pythagorean theorem

Let's prove the Pythagorean theorem by adding up the areas.

In the above image, the square with the side (a + b) is made up of a square with side c, and four right triangles with sides a, b, and c. Let's find the area of this square using two different strategies:

1. The surface area of the square with the side length (a + b) can be calculated as (a + b)²:

A = (a + b)²

2. The same surface area can be found as the sum of the surface areas of the figures making the square – the area of a square with side c, and four areas of a triangle with sides a, b, and c. The area of the square with side c can be calculated as c². The area of the right triangle with sides a, b, and c can be found as (ab)/2. Therefore,

A = c² + 4 × (ab)/2 = c² + 2ab

Since both of these calculations describe the same surface area, we can equate them:

(a + b)² = c² + 2ab

Expanding the square on the left side of the equation, we get:

a² + 2ab + b² = c² + 2ab

Subtracting 2ab from both sides of the equation, we get:

a² + b² = c²

which is the required result.

Calculation algorithms

Finding the sides of a right triangle

If two sides of a right triangle are given, the third side can be found using the Pythagorean theorem. For example, if sides a and b are given, the length of side c can be found as follows:

$$c=\sqrt{a²+b²}$$

Similarly,

$$a=\sqrt{c²-b²}$$

and

$$b=\sqrt{c²-a²}$$

Finding the angles of a right triangle

If all three sides of the right triangle are known, the non-90° angles of the triangle can be found as follows:

• ∠α = arcsin(a/c) or ∠α = arccos(b/c)
• ∠β = arcsin(b/c) or ∠β = arccos(a/c)

Here, ∠α is the angle opposite the leg 'a', ∠β is the angle opposite the leg 'b', and 'c' is the hypotenuse. The choice between arcsin and arccos depends on which leg (a or b) you are considering in relation to the angle. Using arcsin, you use the opposite leg to the angle, and with arccos, you use the adjacent leg to the angle. Both approaches are valid and will give you the correct angle measurements in a right triangle.

Area of a right triangle

The area of a right triangle can be calculated as 1/2 of the product of its legs:

A = 1/2 × (ab) = (ab)/2

Perimeter of a right triangle

The perimeter of a right triangle is calculated as a sum of all its sides:

P = a + b + c

Altitude to hypotenuse

If all three sides of a right triangle are known, the altitude to hypotenuse, h, can be found as follows:

h = (a × b)/c

Real-life examples

The pythagorean theorem is widely used in architecture and construction to calculate the lengths of the necessary component and ensure the angles in constructed buildings are right. Let's look at an example of applying the theorem.

Fitting objects

Imagine you are moving, and you hired a moving truck with a length of 4 meters and a height of 3 meters. You don't have many bulky items, but you do own a ladder, which is 4.5 meters long. Will your ladder fit into the truck?

Solution

Since the ladder length, 4.5 meters, exceeds the length of the truck, 4 meters, the only way the ladder will fit inside is diagonal. To determine whether that's possible, we need to use the Pythagorean theorem to calculate the hypotenuse of a triangle with the sides equal to the length and height of the truck. Therefore, in our case a = 4, b = 3, and we need to find c:

$$c=\sqrt{a²+b²}=\sqrt{4²+3²}=\sqrt{16+9}=\sqrt{25}=5$$

The hypotenuse of a triangle with a = 4 and b = 3 is c = 5. Therefore, the longest object that can fit into the truck can be 5 meters. Your ladder is 4.5 meters long. Therefore, it will easily fit!

Answer

Yes, the ladder will fit.

Additional calculations

This online calculator will also find some additional characteristics of the given triangle. Calculate these characteristics for the triangle with a = 4, b = 3, and c = 5.

Area of the triangle:

A = (ab)/2 = (3 × 4)/2 = 12/2 = 6

Perimeter of the triangle:

P = a + b + c = 3 + 4 + 5 = 12

Altitude to hypotenuse:

h = (a × b)/c = (3 × 4)/5 = 12/5 = 2.4

Angle opposite to side a:

∠α = arcsin(a/c) = arcsin(4/5) = arcsin(0.8) = 53.13° = 53°7'48" = 0.9273 rad

Angle opposite to side b:

∠β = arcsin(b/c) = arcsin(3/5) =arcsin(0.6) = 36.87° = 36°52'12" = 0.6435 rad