No results found
We can’t find anything with that term at the moment, try searching something else.
Right Triangle Calculator
Right triangle calculator finds missing triangle measurements. It calculates side lengths, angles, perimeter, area, altitude-to-hypotenuse, inradius, and circumradius.
| Result | |||
|---|---|---|---|
| a | 3 | ||
| b | 4 | ||
| c | 5 | ||
| h | 2.4 | ||
| α | 36.8699° = 0.6435011 rad | ||
| β | 53.1301° = 0.9272952 rad | ||
| area | 6 | inradius | 1 |
| perimeter | 12 | circumradius | 2.5 |
There was an error with your calculation.
Table of Contents
- Right triangle calculator
- Limitations on the input values of the triangle calculator
- Right triangle: definition and helpful information
- The Pythagorean theorem
- Other essential formulas
- Calculation example
- Special right triangles

Right triangle calculator
The right triangle calculator is an online triangle solver focusing only on the right triangles. The calculator takes any two values of the right triangle as input and calculates the missing triangle measurements. The included values are – the lengths of the sides of the triangle (a, b and c), the angle values except for the right angle (α and β), perimeter (P), area (A), and altitude-to-hypotenuse (h).
To use the calculator, enter any two of the values listed above and press "Calculate".
The angle values can be input both in degrees and in radians. To input the value in radians using π, use the following notation: "pi." For example, if the given angle value is π/3, insert "pi/3."
The calculator will show all the missing values and the calculation steps. The calculator will also demonstrate the scaled view of the relevant triangle, and the values of the inradius and the circumradius.
Limitations on the input values of the triangle calculator
- You can only input two values.
- The angle values of α and β should be less than 90° or (π/2)rad.
- The length of the altitude-to-hypotenuse (h) should not exceed the length of any catheti (a or b).
- The length of each side of the triangle (a, b, or c) must be less than the sum of the other two sides.
- For any given hypotenuse length, the triangle has a maximum perimeter. The calculator will not accept any perimeter exceeding this value. The maximum perimeter of the right triangle with the given hypotenuse length corresponds to the case of an isosceles triangle (a=b). In this case \$a=b=\frac{c}{\sqrt2}\$, and the maximum perimeter \$P=a+b+c=c+\frac{2c}{\sqrt2}\$.
Right triangle: definition and helpful information
A right triangle is a triangle where one angle equals 90° or \$\frac{π}{2}\ rad\$. The side opposite the right angle is called the hypotenuse. The other two sides are called the catheti, or legs, of the triangle.
The leg b is sometimes called the base of the right triangle, and the leg a is the right triangle's height.
The legs of the triangle are always shorter than the hypotenuse. Since one angle of the triangle equals 90°, and the sum of all angles of any triangle is 180°, the sum of the other two angles of the right triangle is also 90°: α+β=90°. The lengths of the sides of the triangle are related to each other as it is described in the Pythagorean theorem.
The Pythagorean theorem
The Pythagorean theorem relates the lengths of all sides of a right triangle. It states that the square of the hypotenuse equals the sum of the squares of the two legs:
$$c^2=a^2+b²$$
Consequently, if only the lengths of the catheti are known, the length of the hypotenuse can be calculated as follows:
$$c=\sqrt{a^2+b²}$$
Suppose we know the length of one cathetus and the length of the hypotenuse. In that case, we can calculate the length of the other cathetus as follows:
$$a=\sqrt{c^2-b²}$$
$$b=\sqrt{c^2-a^2}$$
The Pythagorean theorem is the most important theorem about the right triangle and one of the most important theorems in Euclidean geometry.
Other essential formulas
Apart from the Pythagorean theorem, the following relations are used to calculate the missing values of a right triangle:
The perimeter of a triangle is the sum of the lengths of all its sides and is found as
$$P = a + b + c$$
The area of a right triangle is calculated as
$$A=\left( \frac{1}{2} \right)ab$$
To find the angles of the right triangle, we should calculate the angles' sine, cosine, and tangent. To find the sine, cosine, or tangent of an angle, we need to identify the adjacent and opposite sides of the angle. A hypotenuse and one other side form both acute angles of the right triangle. This other side is the adjacent side of the corresponding angle. The side that is left is thus the opposite side of this angle. For example, in the figure below, a is the opposite side of angle α, and b is the adjacent side.
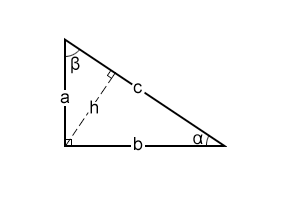
The sine of any acute angle in the right triangle can be found as the length of the opposite side divided by the length of the hypotenuse:
$$\sin{\alpha}=\frac{a}{c}, \sin{\beta}=\frac{b}{c}$$
The cosine of any acute angle in the right triangle can be calculated as the length of the adjacent side divided by the length of the hypotenuse:
$$\cos{\alpha}=\frac{b}{c}, \cos{\beta}=\frac{a}{c}$$
The tangent of any acute angle in the right triangle can be found as the ratio of the length of the opposite side to the length of the adjacent side:
$$\tan{\alpha}=\frac{a}{b}, \tan{\beta}=\frac{b}{a}$$
The length of the altitude-to-hypotenuse is calculated as
$$h=\frac{ab}{c}$$
The calculator also finds the radius and perimeter of a given triangle using the following formulas:
$$Inradius=\frac{ab}{a+b+c}$$
$$Circumradius=\frac{c}{2}$$
Calculation example
Let's assume we have a triangle where the lengths of the two legs are known: a = 3 and b = 4. Let's find all the missing values of the triangle.
First, let's find the length of the hypotenuse c by using the Pythagorean theorem:
$$c=\sqrt{a^2+b²}=\sqrt{3^2+4^2}=\sqrt{9+16}+\sqrt{25}=5$$
$$c=5$$
Now, let's find the angle values of the triangle. As mentioned above,
$$\sin{\alpha}=\frac{a}{c}$$
therefore,
$$\alpha=arcsin\left(\frac{a}{c}\right)$$
$$\alpha=arcsin\left(\frac{3}{5}\right)=arcsin(0.6)=0.6435\ rad\ =\ 36.87° = 36°52'12"$$
Similarly
$$\sin{\beta}=\frac{b}{c}$$
therefore
$$\beta=arcsin\left(\frac{b}{c}\right)$$
$$\beta=arcsin\left(\frac{4}{5}\right)=arcsin(0.8)=0.9273\ rad\ =\ 53.13° = 53°7'48"$$
Let's find the altitude-to-hypotenuse, h:
$$h=\frac{ab}{c}=\frac{3×4}{5}=\frac{12}{5}=2.4$$
For the area of the triangle, we have:
$$A=\frac{1}{2}ab=\frac{a× b}{2}=\frac{3×4}{2}=6$$
For the perimeter of the given triangle, we have:
$$P = a + b + c = 3 + 4 + 5 = 12$$
The inradius can be calculated as follows:
$$inradius=\frac{ab}{a+b+c}=\frac{3×4}{3+4+5}=\frac{12}{12}=1$$
And finally, the circumradius:
$$circumradius=\frac{c}{2}=\frac{5}{2}=2.5$$
Special right triangles
There are two special types of right triangles – the 45-45-90 triangle and the 30-60-90 triangle. The lengths of the sides of these triangles are in a special ratio.
The isosceles right triangle
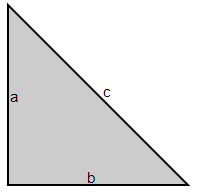
The right triangle with the measures of acute angles of 45° and 45° has two equal angles. Therefore, the lengths of its legs are also equal, making this triangle isosceles and right. The lengths of its sides are related as follows:
$$a : b : c = 1 : 1 : \sqrt{2}$$
The 30-60-90 triangle
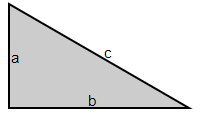
The acute angles of this triangle are 30° and 60°. The lengths of its sides are related as follows:
$$a : b : c = 1 : \sqrt{3} : 2$$
where 'a' is the side opposite the 30° angle, 'b' is the side opposite the 60° angle, and 'c' is the hypotenuse.