Slope Calculator

Slope Calculator

The slope calculator is an intuitive online tool designed to help you quickly find the slope of a straight line. In mathematics, the slope of a line is defined as the ratio of the change in the vertical coordinate (the y-coordinate) relative to the change in the horizontal coordinate (the x-coordinate)—often referred to as "rise over run." Whether you are a student, engineer, or math enthusiast, this tool simplifies complex coordinate geometry calculations.

Used Notation

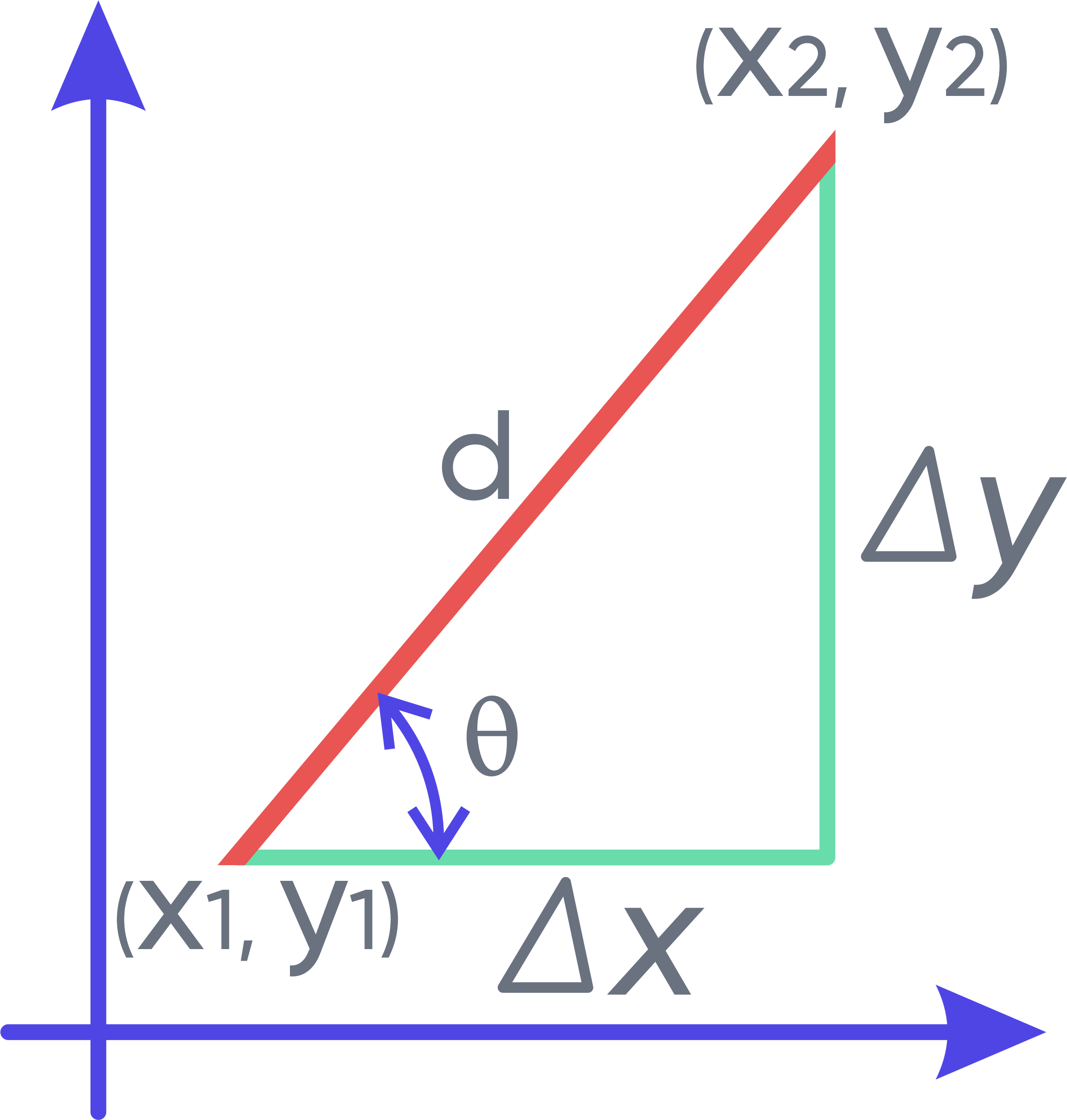
The slope is universally denoted by the letter m. The graphical plot above illustrates all the standard notations utilized in our calculator. This versatile slope finder can perform precise calculations in two primary scenarios:

1. When the coordinates of two points on the line are known: On a Cartesian plane, these two points have the coordinates (x₁,y₁) and (x₂,y₂). In this scenario, the calculator will accurately determine the slope of the line, m.

2. When one point and the slope are known: If you know the coordinates of a single point (x₁,y₁), the distance d, and the slope of the line, the calculator will compute the exact coordinates of the second point on the line, (x₂,y₂).

In both scenarios, the calculator will also return other essential characteristics of the line: the horizontal change (or run) ∆x, the vertical change (or rise) ∆y, the inclination angle θ, and the overall line length or distance, d.

Directions for Use

To get started, identify your known values and select the appropriate calculation method from the top menu. If you have the exact coordinates of two points, select “If the 2 Points are known.”

If you only have the coordinates of a single point, you will need to know the distance, d, and the slope of the line, m, to perform the calculation. In this case, select “If 1 Point and the Slope are known.”

If the 2 Points are Known

Enter the known coordinates of your points into the corresponding fields, then click “Calculate.” The slope finder will instantly return the following information:

• the slope m,
• the inclination angle θ,
• the length of the line d,
• the horizontal change ∆x,
• the vertical change ∆y.

For educational purposes, the calculator also displays the step-by-step formulas used to find the slope and all other characteristic values. Additionally, it will generate the corresponding equation of the line and plot a schematic graph for a clear visual representation.

If 1 Point and the Slope are Known

Enter the known coordinates of your starting point, the distance, and the slope into the respective fields. Note that instead of the standard slope, you can opt to insert the value of the “angle of incline (theta or θ).” The value of θ must be entered in degrees. You only need to provide one of these values (either m or θ). If both m and θ are entered, the calculator will ignore the θ value and prioritize the slope m for its calculations.

Click “Calculate.” The calculator will return the coordinates of the second point (x₂,y₂), the horizontal change ∆x, the vertical change ∆y, and the length of the line d. If you used the slope m for your input, the tool will also return the angle of incline θ. Conversely, if you used the angle of incline θ, it will compute and return the slope m. Finally, the tool will display the standard equation of the line and generate a visual plot of the graph.

Slope Formula

As defined above, the slope of a line represents the change in the vertical coordinate (y-coordinate) relative to the change in the horizontal coordinate (x-coordinate). This relationship is expressed as:

$$m=\frac{y₂-y₁}{x₂-x₁}=\frac{∆y}{∆x}=tanθ$$

This central equation is known as the slope formula. We can use it to manually calculate the slope of any straight line if the coordinates of two points on that line are known. The slope, universally denoted as m, describes both the direction and the steepness of a line:

• If the line goes upwards from left to right, then y₂>y₁ when x₂>x₁. The slope will always be positive, m>0. In this case, we say that the line is increasing.

• If the line goes downwards from left to right, then y₂ < y₁ when x₂ > x₁. The slope will be negative, m < 0. In this case, we say that the line is decreasing.

• If the line is horizontal, then y₂=y₁ and y₂-y₁=0. Then the slope will also equal zero: m=0.

• If the line is vertical, then x₂=x₁ and x₂-x₁=0. The slope formula will have a zero in the denominator, and the slope is undefined.

Line Equation

We can express any linear equation in the following standard format:

$$y=mx+b$$

This popular format is called the slope-intercept form. When plotted, this equation creates a straight line where m represents the slope. The variable b represents the coordinate at which the graph intercepts the y-axis. For this reason, b is commonly called the y-intercept, since y=b when x=0.

Alternatively, when the slope and the coordinates of a single point on the line are known, we can write the line equation in the point-slope form:

$$y-y₁=m(x-x₁)$$

This structural form of the linear equation is highly beneficial for manually finding the y-intercept of a given line.

Calculation Example

Let’s walk through a practical example assuming we know the exact coordinates of two points on a line.

Given:

$$x₁=1$$

$$y₁=1$$

$$x₂=9$$

$$y₂=25$$

First, let’s use the slope formula to find the slope of this line:

$$m=\frac{y₂-y₁}{x₂-x₁}=\frac{∆y}{∆x}$$

$$m=\frac{25-1}{9-1}=\frac{24}{8}=3$$

$$m=3$$

Now, let’s calculate the remaining characteristic values of the line. Since we know that m=tanθ, we can determine the angle of incline θ as follows:

$$\theta=\arctan{\left(m\right)} = \arctan\frac{∆y}{∆x} = 71.565051177078°$$

Furthermore,

$$∆x=9-1=8$$

$$∆y=25-1=24$$

We can determine the distance d between the two points using the Pythagorean theorem. This fundamental geometric principle states that the square of the hypotenuse's length equals the sum of the squares of the right triangle's legs.

Applying this theorem to our right triangle, we get:

$$d^2=∆x^2+∆y^2$$

Therefore,

$$d=\sqrt{∆x^2+∆y^2}$$

$$d=\sqrt{8^2+{24}^2}=\sqrt{640}$$

$$d=25.298221281347$$

To find the y-intercept of the line, let’s format our line equation into the point-slope form, substituting our given values for m, x₁, and y₁:

$$y-1=3\left(x-1\right)$$

$$y=3x-2$$

Therefore, y=-2 is the y-intercept of the line. In other words, when x=0, y=-2.

To find the x-intercept, if y=0:

$$x=\frac{2}{3}=0.66666666666667$$

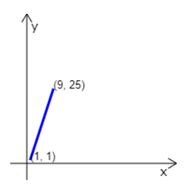
This sketch visually represents the corresponding line. In our example, the slope is positive, m>0, and we can clearly see that the line is increasing—moving upward from left to right. We can also observe that the line is quite steep, which perfectly aligns with our calculated inclination angle of θ ≈ 72°.