LCM Calculator

This online LCM calculator allows you to find the least common multiple of two or more numbers. The least common multiple is the smallest number, which is a multiple of all given numbers. For example, the LCM of 2 and 3 would be 6 since 6 is the smallest number that is evenly divisible by both of the given numbers – 2 and 3. The calculator also demonstrates the detailed solutions for finding LCM using various methods: listing multiples, prime factorization, cake/ladder, division method, GCF method, and Venn diagram.

Directions for Use

• To use the LCM calculator, input the numbers and press “Calculate.”
• Use spaces or commas to separate your numbers. Note that you can’t use commas within a number. For example, you should write one thousand as 1000, not 1,000. The calculator will immediately display the least common multiple of the input numbers.
• To view a detailed solution, choose the solution method from the drop-down menu and press “Calculate.”
• If you want to see the solution steps for a different method, make the relevant choice in the drop-down menu and press “Calculate” again.

Calculation Algorithms

Listing multiples

The most straightforward way of finding the least common multiple of several numbers is to write down lists of multiples for each given number until one of the multiples appears on all lists. That multiple will be LCM.

For example, let’s find LCM of 5 and 7, or LCM (5, 7):

Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, etc.

Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, etc.

35 is the first multiple appearing in both lists; therefore, LCM (5, 7) = 35.

Prime factorization

To find the LCM of several numbers by prime factorization, follow the steps below:

1. Write down the prime factors of each number.
2. Write down the prime factorization of each number in the exponent form (for example, 2 × 2 × 2 would be 2³).
3. Multiply the highest powers of all prime factors.
4. The resulting number would be the LCM of the given numbers.

Note that you can find LCM without expressing prime factorization in the exponent form. In that case, you will replace step 3 by multiplying each prime factor a maximum of times that it occurs for any one given number.

For example, let’s find the LCM of 3, 12, 40, LCM (3, 12, 40):

1. Finding prime factors of each number.

Prime factors of 3: 3 is prime.

Prime factors of 12: 2 × 2 × 3

Prime factors of 40: 2 × 2 × 2 × 5

2. Writing prime factorization in exponent form.

3 = 3¹

12 = 2² × 3

40 = 2³ × 5¹

3. Multiplying the highest powers of all prime factors.

2³ × 3¹ × 5¹ = 120

4. LCM (3, 12, 40) = 120

Without the exponent form, step 3 would become 2 × 2 × 2 × 3 × 5 = 120.

The LCM calculator will demonstrate both of these options for the prime factorization solution algorithm.

Cake/Ladder

This method got its name because the resulting solution algorithm resembles a cake (or a ladder!). Let’s look at this algorithm by immediately using an example and finding LCM of 12, 15, and 24.

1. First, write the given numbers next to each other, and draw a “ladder step” or a “cake layer around them,” like this:

2. Find a number that can evenly divide at least two of the given numbers. Write it down to the left of the given number, and perform the division. Write down the division results in the following “cake layer.” If one of the numbers is not divisible, keep it.

Let’s use 2 as the first number in our example since both 12 and 24 are divisible by 2. We will get the following picture:

3. Keep repeating step 2, until there are no more numbers that can evenly divide any two of the given numbers:

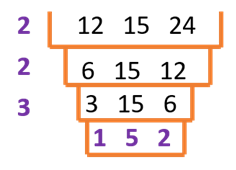
4. The LCM of the given numbers will be the product of the numbers from the left column and the bottom row. In our case:

LCM (12, 15, 24) = 2 × 2 × 3 × 1 × 5 × 2 = 120

Division method

The division method is very similar to the cake/ladder method. Still, here you keep performing divisions as long as any one of the given numbers is divisible by a prime number. As a result, the bottom row will consist only of ones, and you can find LCM by multiplying all numbers from the left column. If we look at the previous example of finding LCM (12, 15, 24), the division table will look like this:

2	12	15	24
2	6	15	12
2	3	15	6
3	3	15	3
5	1	5	1
	1	1	1

And finally, LCM (12, 15, 24) = 2 × 2 × 2 × 3 × 5 = 120

GCF method

To find the LCM of two numbers with the help of GCF, use the following formula:

LCM (x, y) = (x × y) / GCF (x, y)

You should iterate the above formula to find the LCM of more than two numbers. For example, the LCM of three numbers can be found as follows:

LCM (x, y, z) = LCM (LCM (x, y), z)

For example, let’s find LCM of 6 and 8. The GCF (6, 8) is 2. Therefore,

LCM (6, 8) = (6 × 8)/2 = 48/2 = 24

Venn diagram

To find LCM using Venn diagrams, you will need to start by identifying the prime factors of each number. Then you need to group those factors based on their affiliation with two or three of the given numbers and draw them as a Venn diagram. For LCM (12, 15, 24), the diagram will look like this:

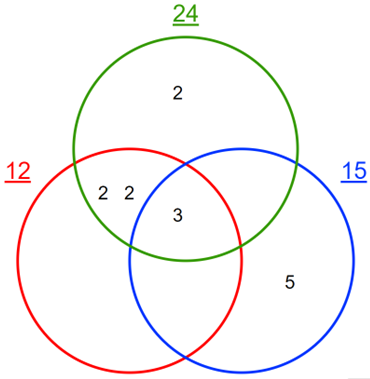
Note that the online calculator will only show the Venn diagram solution for 2 or 3 numbers.

Calculation example

Mike and Lina both attend karate lessons. However, their schedules are different: Mike goes every 5 days, while Lina goes every 3 days. Today they attended the lesson together. How many days will pass until they attend a class together again?

Solution

To solve this problem, we need to find the least common multiple of 5 and 3, LCM (5, 3). Let’s do it with the help of the prime factorization method.

3 is prime, therefore 3 = 3¹

5 is also prime, therefore, 5 = 5¹

LCM (5, 3) = 3¹ × 5¹ = 15

Answer

Mike and Lina will go to a karate lesson together in 15 days.